Giải đề thi thử đại học môn Toán (khối A) năm 2012 – Trường Chuyên Quốc Học Huế
Mỗi câu của đề thi được giải trên một trang.
Hãy click vào các số trang cuối bài viết nàu để xem !
Câu I:
1). Khảo sát sự biến thiên và vẽ đồ thịcủa hàm số
.
2). Đường thẳng vuông góc với trục tung tạicắt đồ thị
tại ba điểm phân biệt
với hoành độ của
là số âm. Tìm tung độ của điểm
sao cho
.
Giải:
Câu I.2.
Gọi tọa độ của . Đường thẳng
qua
và vuông góc với trục tung có phương trình
.
Phương trình hoành độ giao điểm của và
là
.
Dựa vào đồ thị ta nhận thấy
cắt
tại 3 điểm phân biệt khi và chỉ khi
.
Với điều kiện trên thì cắt
tại 3 điểm phân biệt
trong đó có một điểm có hoành độ âm. Gọi
theo thứ tự là hoành độ các điểm
. Ta có
và .
Mặt khác ta có .
Từ giả thiết suy ra (vì
).
Giải (1) và (4) ta được .
Thay (5) vào (2) ta được .
Thay (5), (6) vào (3) ta được: (thỏa điều kiện
).
Vậy giá trị của cần tìm là
.
Posted on 12/04/2012, in ôn thi đại học and tagged giải đề thi thử đại học môn toán. Bookmark the permalink. 24 bình luận.

G(2)=1/6
ThíchThích
Thầy sửa lại rồi. Cảm ơn em !
ThíchThích
Thầy cho em hỏi,ở ý (1),(2),(3) là dựa theo công thức gì mà có được ạ.Cảm ơn thầy!
ThíchThích
Dựa theo định định lý Viet cho phương trình bậc ba một ẩn em à.
(Không được đề cập trong chương trình toán phổ thông)
———–
Nếu không dùng định lý này em có thể giải theo cách sau:
Với là các nghiệm của phương trình
là các nghiệm của phương trình  , ta có:
, ta có:



 em sẽ tìm được
em sẽ tìm được 
EM giải hệ gồm ba phương trình trên và phương trình
ThíchThích
Thầy ơi vì sao MN =x1 và PQ =X3-x2
ThíchThích
Vì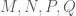 đều nằm trên đường thẳng
đều nằm trên đường thẳng 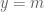 nên có tung độ bằng nhau và bằng
nên có tung độ bằng nhau và bằng  .
. .
. như trên.
như trên.
Tức là
Từ đó em tính được
ThíchThích
Thầy ơi! Giải giúp em bài toán này, dạ em cần gấp Thầy ơi:
5^x+2.5^x/căn(5^(2x)-4)>=3.căn5
ThíchThích
Điều kiện của bất phương trình: .
. ta có điều kiện
ta có điều kiện  và
và  . Giải ta được
. Giải ta được 
 .
.



 ta có
ta có  .
.
 trở thành
trở thành 


 , giải bất phương trình
, giải bất phương trình  ta được
ta được  hoặc
hoặc 
 hoặc
hoặc  .
. hoặc
hoặc  .
.
 hoặc
hoặc  , với
, với  .
.
 hoặc
hoặc  .
. hoặc
hoặc  .
.
 hoặc
hoặc  .
.
![(\log_5{2}; \dfrac{1}{2} ] \cup [ \log_5{2\sqrt{5}}; +\infty)](https://s0.wp.com/latex.php?latex=%28%5Clog_5%7B2%7D%3B+%5Cdfrac%7B1%7D%7B2%7D+%5D+%5Ccup+%5B+%5Clog_5%7B2%5Csqrt%7B5%7D%7D%3B+%2B%5Cinfty%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.
Đặt
Bất phương trình đã cho trở thành
Đặt
{Giải bằng máy tính bỏ túi để dò tìm nghiệm của vế trái, từ đó ta phân tích được}
Với
Do đó ta có
Suy ra
Từ đó ta có
Vậy tập nghiệm của bất phương trình đã cho là
ThíchThích
Dạ! Em cảm Thầy nhiều!!!!
ThíchThích
Thầy ơi ! câu lượng giác có đúng đề không ạ …. em thấy trên trang vnmath.vn cho đề là : (1 + (1 + 2sinx).cosx = 2[ (cosx)^2 + (cosx)^4 ] +1
ThíchThích
II/ 1/ thầy: câu lượng giác sai ở chổ cosx và cos2x phân tích dòng 2: cos2x=1-2sin^2x chổ đó là cosx .. (bài này giải ra vô nghiệm) “copy sai đề”
ThíchThích
thua thay, dao ham g'(t) phaj bang te^t+e^t chu a?
(Em onl bang dđ nen k go dau, thay thong cam!)
ThíchThích
thay oi sao bai luong giac, em dat (cosx)^2(1+1-(sinx)^2)lai khong giai ra a?
ThíchThích
đề bài lượng giác hình như sai rồi thầy ơi. (1+2sinx)cos x= 2(cos^2 x + cos^4 x)+1. Em tải trên vnmath như vậy mà.
ThíchThích
em nhìn nhầm.hì. em cảm ơn thầy
ThíchThích
sai thật mà. thầy xem lại đi thầy ơi.hix. đề trong vnmath khác
ThíchThích
Thầy ơi thầy giúp tụi em giải đề thi thử toán khối D của trường Quốc Học Huế được không thầy? Em thấy blog chỉ đăng đề và đáp án khối A, B thôi, huhu
ThíchThích
Em gửi cho thầy đề được không, thầy không có đề khối D em à.
ThíchThích
dạ link đề thi đây: http://onluyentoan.vn/showthread.php?t=4036 thầy giúp tụi em nhe thầy! em cám ơn thầy trước 🙂
ThíchThích
g'(t) đạo hàm hình như sai rùi thầy ơi.
ThíchThích
Câu giải bpt đó thầy
ThíchThích
thầy ơi tại sao x1 + x2 +x3 =3 ạ???
ThíchThích
Bon kia ngu that he thuc vi-et phuong bac 3 ma ko piet. Thay dau co thoi jan tra loi may caj thu vo van day.
ThíchThích
Thay oj hinh phang 10 sao kho ru vay. Cho zat lang nhang nam de nam laj wa kho
ThíchThích