Toán 12

Một số sai lầm cơ bản thường gặp phải khi giải toán.

Bài 1: Tính đạo hàm của hàm số $y= \sqrt{x-x^2}$ .

Nhận xét: Đối với bài toán này nhiều học sinh thấy rất đơn giản nhưng thường gặp phải những sai lầm, thiếu sót rất cơ bản sau:
– Quên tìm tập xác định của hàm số;
– Bởi vì tính đạo hàm theo công thức và các quy tắc nên Khi kết luận không để ý đến các điểm tại đó hàm số không có đạo hàm (đạo hàm không xác định).

Lời giải:

Ý1: Tập xác định: $D= [0; 1]$ .

Ý2: Ta có $y'= \dfrac{(x-x^2)'}{2\sqrt{x-x^2}}= \dfrac{1-2x}{2\sqrt{x-x^2}}$ với mọi $x \in (0;1)$ .
Lưu ý: Trong bước này học sinh thường không chú ý rằng vì lúc này đạo hàm hàm số có chứa ẩn ở mẫu nên cần để ý điều kiện để mẫu số khác không. Trong Bài toán này ta đã loại bỏ 2 điểm $x=0, x=1$ tại đó đạo hàm không xác định.

Ý3: Kết luận: Vậy $y' = \dfrac{1-2x}{2\sqrt{x-x^2}}$ , với mọi $x \in (0;1)$ . Hàm số không có đạo hàm tại $x=0 , x=1$ .

Bài 2: Tìm các điểm cực trị (nếu có) của hàm số $y=f(x)= \sin^2{2x}$ .

Giải:

Ý1: Tập xác định: $D= \mathbb{R}$ .

Ý2: Ta có:

$y'= 2 \sin{2x}. 2 \cos{2x} = 2 \sin{4x}$

$y'=0 \Leftrightarrow \sin{4x}=0 \Leftrightarrow 4x=k \pi \Leftrightarrow x=k \dfrac{ \pi}{4} , k \in \mathbb{Z}$ .

Ý3: Mặt khác $y'' = 8 \cos{4x}$ .
Ta có $y'' (k \dfrac{ \pi}{4}) = 8 \cos(k \pi)$ .
Suy ra: – $y'' (k \dfrac{ \pi}{4}) = 8 \cos{2n \pi} =8$ nếu $k=2n$ .
– $y'' (k \dfrac{ \pi}{4})= 8 \cos{(2n+1) \pi} = -8$ nếu $k=(2n+1)$ .

Ý4: Kết luận:
– Hàm số đạt cực đại tại các điểm $x= 2n \dfrac{ \pi}{4} =n \dfrac{ \pi}{2}$ .
– Hàm số đạt cực tiểu tại các điểm $x= (2n+1) \dfrac{ \pi}{4}$ . Với $n \in \mathbb{Z}$ .

Nhận xét: Sai lầm của các em học sinh là thường kết luận $y'' (k \dfrac{ \pi}{4}) = 8$ nếu $k$ chẵn, và $y'' (k \dfrac{ \pi}{4}) = -8$ nếu $k$ lẻ . Bởi vì nếu chỉ xét $k$ chẵn và lẻ thì bỏ sót giá trị $k=0$ .

Bài tập tương tự: Tìm các điểm cực trị (nếu có) của hàm số $y=f(x)= \cos^2{3x}$ .

*** Các bước khảo sát hàm số: Củng cố, ôn tập, hệ thống sơ đồ khảo sát các hàm số cơ bản giúp các em học sinh dễ nhớ, dễ làm. Xem tiếp…

Bình luận về bài viết này
Comments 25

cô đơn | 02/10/2008 lúc 06:05

Mấy bài lượng giác nỳ thiệt là quá khó chịu…. ngang đoạn đạo hàm bậc 2 khó hiểu quá Thầy ơi?

ThíchThích

Trả lời
cAu_Ut | 11/10/2008 lúc 22:57

thanks all!!!

ThíchThích

Trả lời
NguyenThanhLong | 16/10/2008 lúc 11:52

cach tim m de ham so co cuc tri hoac 2 cuc tri hoac khong co cuc tri

ThíchThích

Trả lời
caolong | 17/10/2008 lúc 13:06

Dạng toán này còn phụ thuộc vào hàm số loại nào (hàm số bậc ba, bậc bốn hya hàm phân thức hữu tỷ). Các em có 2 căn cứ là 2 điều kiện đủ ở SGK.
Em có thể đưa lên một đề bài toán cụ thể rồi thầy sẽ viết rõ và giải thích kỹ hơn.

ThíchThích

Trả lời
vu hoang tung | 09/12/2008 lúc 10:54

em thua thay,trong nay thay co day ve nguyen ham ko a…em cam on.

ThíchThích

Trả lời
- caolong | 13/12/2008 lúc 01:34
  
  Chào em.
  Rất cảm ơn em đã quan tâm. Chắc chắn là có chứ. Hiện thầy đang bận. Ra Tết học xong mọi thứ thầy sẽ tăng cường viết bài theo yêu cầu của các em. Thầy hứa !
  
  ThíchThích
  
  Trả lời
huy | 15/12/2008 lúc 14:28

hi thay

ThíchThích

Trả lời
lebinh | 29/12/2008 lúc 08:54

anh cao long oi sao em co the nhan ra sai sot trong cac bai khoa sat nhu dk ,tap nghiem va cach xax dinh tcx nua
anh chi ho em, voi

ThíchThích

Trả lời
- caolong | 29/12/2008 lúc 10:50
  
  Chào em !
  Để tránh sai sót trong các bài làm (tự luận) việc đầu tiên là cần nắm vững kiến thức, nắm kỷ các bước Kshs.
  
  Tập xác định (đk xác định) thì không có gì phải để sai cả: Đối với các hàm bậc ba, hàm bậc 4-trùng phương thì TXĐ là $\mathbb{R}$ ; còn với hàm hữu tỷ $y= \dfrac{ax+b}{cx+d}$ thì tìm điều kiện của $x$ để mẫu thức $cx+d\neq 0 \Leftrightarrow x \neq -\dfrac{d}{c}$ , nghĩa là TXĐ là $\mathbb{R} \setminus \{-\dfrac{d}{c}\}$ .
  
  Với tiệm cận, chỉ có hàm số $y= \dfrac{ax+b}{cx+d}$ có tiệm cận (một tiệm cận đứng $x=-\dfrac{d}{c}$ và một tiệm cận ngang $y = \dfrac{a}{c}$ .
  
  Chú ý rằng: Hàm số $y= \dfrac{ax+b}{cx+d}$ có đạo hàm $y'=\dfrac{ad-bc}{(cx+d)^2}$ .
  Do đó nếu $ad-bc >0$ thì $y'>0, \forall x \neq -\dfrac{d}{c}$ nên hàm số luôn đồng biến trên các khoảng $(-\infty; -\dfrac{d}{c})$ , $(-\dfrac{d}{c}; +\infty)$ .
  
  Lưu ý: Không được kết luận, hàm số đồng biến trên tập xác định. Nó chỉ đồng biến trên từng khoảng thuộc tập xác định (các khoảng này không giao nhau).
  Trường hợp $y'<0$ thì kết luận hàm số nghịch biến trên các khoảng đã chỉ trên.
  
  Chúc em học tốt !
  
  ThíchThích
  
  Trả lời
chemistry lovers | 21/04/2011 lúc 00:06

Đây là các video dạy học các môn Toán, Lý, Hóa
ở cấp bậc phổ thông do các giáo sư nổi tiếng giảng dạy.
Các bạn có thể download ở đây
http://all365climaxdays.blogspot.com/

ThíchThích

Trả lời
thu hang | 30/11/2011 lúc 19:49

thay oi em nho thay giai cho em may bai nay cai a:
1.a.giai he phuong trinh: y+xy^2=6x^2
1+x^2y^2=5x^2
b.tim min cua y=can cua (x^2+4x+8)+ can cua (x^2+2x+2)
2.tim tren truc tung diem M sao cho MA+MB min biet A(1;2), B(-2;-4)
em cam on thay nhe!

ThíchThích

Trả lời
- caolong | 30/11/2011 lúc 22:19
  
  Câu 1: Ta có $\left\{ \begin{array}{l} y + x{y^2} = 6{x^2} \\ 1 + {x^2}{y^2} = 5{x^2} \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} y\left( {1 + xy} \right) = 6{x^2} \\ 1 + {x^2}{y^2} = 5{x^2} \\ \end{array} \right.$ (*)
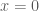  Nhận thấy $x=0$ không thỏa mãn hai phương trình của hệ, do đó ta có:
  
  $\Leftrightarrow \left\{ \begin{array}{l} \dfrac{y}{x}\left( {\dfrac{1}{x} + y} \right) = 6 \\ \dfrac{1}{{{x^2}}} + {y^2} = 5 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \dfrac{y}{x}\left( {\dfrac{1}{x} + y} \right) = 6 \\ {\left( {\dfrac{1}{x} + y} \right)^2} - 2\dfrac{y}{x} = 5 \\ \end{array} \right.$
  Đặt $a = \dfrac{y}{x};b = \dfrac{1}{x} + y$ , hệ (*) trở thành
  $\left\{ \begin{array}{l} a.b = 6 \\ {b^2} - 2a = 5 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left( {{b^2} - 5} \right)b = 12 \\ 2a = {b^2} - 5 \\ \end{array} \right.$
  
  $\Leftrightarrow \left\{ \begin{array}{l} {b^3} - 5b - 12 = 0 \\ 2a = {b^2} - 5 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left( {b - 3} \right)\left( {{b^2} + 3b + 4} \right) = 0 \\ 2a = {b^2} - 5 \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} b = 3 \\ a = 2 \\ \end{array} \right.$
  Vậy, từ cách đặt ta có hệ đã cho tương đương với $\left\{ \begin{array}{l} \dfrac{y}{x} = 2 \\ \dfrac{1}{x} + y = 3 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ne 0 \\ y = 2x \\ 1 + 2{x^2} = 3x \\ \end{array} \right.$
  
  $\Leftrightarrow \left\{ \begin{array}{l} x = 1 \\ y = 2 \\ \end{array} \right.$ hoặc $\left\{ \begin{array}{l} x = \dfrac{1}{2} \\ y = 1 \\ \end{array} \right.$
  —–
  Kết luận: Vậy hệ đã cho có 2 nghiệm: $\left( {x;y} \right) = \left( {1;2} \right)$ và $\left( {x;y} \right) = \left( {\dfrac{1}{2};1} \right)$
  
  ThíchThích
  
  Trả lời
- caolong | 30/11/2011 lúc 22:56
  
  Câu 1b;
  Tìm giá trị nhỏ nhất của hàm số: $y=\sqrt{{{x}^{2}}+4x+8}+\sqrt{{{x}^{2}}+2x+2}$ .
  Ta có $y=\sqrt{{{\left( x+2 \right)}^{2}}+{{2}^{2}}}+\sqrt{{{\left( x+1 \right)}^{2}}+{{1}^{2}}}$ .
  Xét điểm $M\left( x;0 \right)$ và hai điểm $A\left( -2;-2 \right)$ và $B\left( -1;1 \right)$ .
  Ta có $y=\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( 0+2 \right)}^{2}}}+\sqrt{{{\left( x+1 \right)}^{2}}+{{\left( 0-1 \right)}^{2}}}=MA+MB$ .
  Khi x thay đổi, ta có M di động trên trục Ox .
  Bài toán đã cho trở thành: Tìm điểm M trên trục hoành sao cho MA+MB nhỏ nhất.
  Với mọi vị trí của M ta luôn có $MA+MB\ge AB$ . (1)
  Nhận xét: A và B nằm khác phía so với trục Ox nên $MA+MB=AB$ khi và chỉ khi M thuộc đường thẳng AB và nằm giữa 2 điểm AB.
  Tức là M là giao điểm của đường thẳng AB với trục hoành. (2)
  Đường thẳng AB có phương trình $(AB): 3x-y+4=0$ .
  Do đó tọa độ của M là nghiệm của hệ $\left\{ \begin{array}{l} 3x - y + 4 = 0 \\ y = 0 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = - \dfrac{4}{3} \\ y = 0 \\ \end{array} \right.$
  .
  Vậy $M\left( -\dfrac{4}{3};0 \right)$ . (3)
  Từ (1), (2) và (3) suy ra $\min \left\{ MA+MB \right\}=AB=\sqrt{10}$ xảy ra tại $M\left( -\dfrac{4}{3};0 \right)$ .
  Vậy giá trị nhỏ nhất của hàm số đã cho là $\min \left\{ y \right\}=AB=\sqrt{10}$ đạt được khi $x=-\dfrac{4}{3}$
  
  ThíchThích
  
  Trả lời
- caolong | 30/11/2011 lúc 23:04
  
  Từ lời giải câu 1b.
  Em hãy giải Câu 2 tương tự như Bài toán phụ trong lời giải câu 1b.
  Em tự giải nhé.
  Đáp số: $M \equiv O\left( {0;0} \right)$
  
  ThíchThích
  
  Trả lời
thu hang | 01/12/2011 lúc 14:49

thay oi cho em hoi duoc khong a bai 1b truoc em hoi thay rang phuong trinh AB la 3x-y+4=0.

ThíchThích

Trả lời
- caolong | 02/12/2011 lúc 07:42
  
  Em viết phương trình đường thẳng $AB$ đi qua điểm $A(-2;-2)$ hoặc $B(-1;1)$ và nhận vectơ $\overrightarrow{AB} =(1;3)$ làm vectơ chỉ phương. Suy ra $\vec{n}=(3;-1)$ là vectơ pháp tuyến.
  Từ đó suy ra phương trình đường thẳng $AB$ là: $3.(x+2)-1.(y+2)=0$
  $\Leftrightarrow 3x-y+4=0$
  
  ThíchThích
  
  Trả lời
thu hang | 03/12/2011 lúc 05:55

thay oi sao bai nay em chi tinh duoc goc C=90 do thoi.tronh khi do co noi goc C co 2 gia tri.thay giai cho em bai nay duoc khong:tim goc C biet c^4-2(a^2+b^2)c^2+a^2b^2+b^4+a^4=0

ThíchThích

Trả lời
- caolong | 03/12/2011 lúc 15:47
  
  Ở đây “tính góc C” ở bài toán nào vậy ?
  Em viết lại đề rõ ràng thầy xem.
  
  ThíchThích
  
  Trả lời
thu hang | 03/12/2011 lúc 17:22

da de yeu cau tinh goc C trong tam giac ABC voi a,b,c la do dai 3 canh cua tam giac thoa man dang thuc tren, ma su dung dinh li sin va cosin trong tam giac thay a.

ThíchThích

Trả lời
- caolong | 03/12/2011 lúc 21:23
  
  Lần sau em cố gắng gỏ Tiếng Việt, có dấu em nhé !
  Gỏ không dấu đọc mệt và khó hiểu lắm !
  
  ThíchThích
  
  Trả lời
Nguyen dinh tung | 02/05/2012 lúc 08:34

Thầy có file .jpg tổng hợp kiến thức chương hình học ko gian ko cho em xin. Mà thầy ơi! E thi khối V nên học kém toán . Nếu muốn kiếm 5đ thi đh thì theo thầy nên tập trung ôn những gì ạ???

ThíchThích

Trả lời
- Đỗ Cao Long | 02/05/2012 lúc 08:42
  
  Những câu thuộc chương trình 12 sẽ giúp em dễ ôn tập, như:
  – Khảo sát hàm số
  – Hình giải tích trong không gian
  – Câu phụ của khảo sát hàm số
  – Tính tích phân
  (- Giải phương trình lượng giác;
  – Hình giải tích trong mặt phẳng.)
  
  ThíchThích
  
  Trả lời
luong ngoc thanh | 15/05/2012 lúc 20:46

thay oi may cach giai do hk co cach nao tom tat nhah hon dc het hak thay

ThíchThích

Trả lời
Văn Lãm Nguyễn | 05/10/2012 lúc 15:35

Em muốn giỏi toán để không ngại khi thày giáo gọi điểm và hiện thức hóa ước nơ khối D

ThíchThích

Trả lời
abc | 03/04/2013 lúc 21:34

k = 0 là số chẵn mà!!!

ThíchThích

Trả lời

	hy trong Đề kiểm tra Hình học 10 (Tham…
	likemath trong Các bước khảo sát hàm số
	likemath trong Các bước khảo sát hàm số
	Lê Văn Hùng trong Giải đề số 2 (Đề thi thử đại h…
	ho thi thu trong Phương trình đường thẳng trong…
	dangloc trong Tính chẵn, lẻ của hàm số
	hatch slack trong Tính chẵn, lẻ của hàm số
	manhhanthtt trong Đề thi tuyển sinh lớp 10 chuyê…
	Khoa trong Đề thi tuyển sinh lớp 10 chuyê…

Đỗ Cao Long's Blog.

Dạy Toán cơ bản cho học sinh yếu môn Toán!

Toán 12

Bình luận về bài viết này

Comments 25

Bình luận về bài viết này Hủy trả lời

Bài viết mới

Xem bài theo Chuyên đề

Các trang chính

Số lượt truy cập

Đang Online

Chào ngày mới

Rank

Giáo dục-Khuyến học (Dân trí)

Top Rated

Liên kết Web

Web học tập

Ý kiến

Đỗ Cao Long's Blog.

Dạy Toán cơ bản cho học sinh yếu môn Toán!

Toán 12

Chia sẻ:

Bình luận về bài viết này

Comments 25

Bình luận về bài viết này Hủy trả lời

Bài viết mới

Xem bài theo Chuyên đề

Các trang chính

Số lượt truy cập

Đang Online

Chào ngày mới

Rank

Giáo dục-Khuyến học (Dân trí)

Top Rated

Liên kết Web

Web học tập

Ý kiến