Tọa độ vectơ
MỘT SỐ BÀI TOÁN CƠ BẢN
Bài 1: Các phép toán vecto và biểu thức tọa độ.
Trong không gian với hệ tọa độ
cho các vectơ
.
Hãy tính tọa độ của vectơ:
.
Bài 2: Cho các vectơ
.
Hãy tính giá trị củađể
2.a).
2.b).
Bài 3:
Trong không gian với hệ tọa độ
cho các vectơ
.
Hãy biểu diễn (phân tích) vectơ
theo 3 vectơ

Bài 4:
Cho hai vecto
. Tìm
sao cho
Bài 5:
Cho 3 điểm
.
5a). Chứng minhlà ba đỉnh của một tam giác.
5b). Tính chu vi của tam giác.
5c). Tìm tọa độ trung điểmcủa
và trọng tâm
của tam giác
.
5d). Tìm tọa độ điểmlà chân đường cao hạ từ đỉnh
của tam giác
.
5e). Tính diện tích tam giác.

cho em hoi :Khi cho biet 2 duong thang cat nhau va co giao diem I va dien tich cua tam giac IAB can tại I,Thi lam sao de tim duoc toa do 2 diem A va B lan luot thuoc 2 duong thang tren
ThíchThích
EM có thể viết phương trình 2 đường thẳng (d1), (d2) về dạng tham số.
 . KHai triển ta được phương trình thứ hai.
. KHai triển ta được phương trình thứ hai.
Gọi tọa độ của A, B theo hai tham số {chẳng hạn A(a; f(a)), B(b, g(b))}.
Sau đó tính trung điểm M của AB. Tính diện tích tam giác IAB bằng
Khai triển ta được một phương trình hai ẩn số a và b;
Mặt khác do tam giác IAB cân tại I nên ta có IM vuông góc với AB.
Tức là
Giải hệ gồm ai phương trình trên, em có thể tìm được a, b rồi suy ra tọa ộ điểm A, B.
ThíchThích
Cho hai vecto . Tìm m để góc giữa hai vecto đó =
. Tìm m để góc giữa hai vecto đó = 
ThíchThích
Áp dụng công thức: .
.
 và
và  ; và góc
; và góc 



 nhé !
nhé !
Trong đó:
Từ đó, ta có
Đến đây, em bình phương hai vế và giải phương trình bậc hai thu được và tìm
ThíchThích
nho thay lam giup em bai nay voi: cho hinh vuong ABCD biet tam I(5/2;5/2).2 diem A,B lan luot thuoc 2 duong thang x+y-3=0 va x+y-4=0.tim toa do cac dinh hinh vuong
ThíchThích
Gọi tọa độ của là
là 
 là
là  ,
,  .
.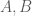 là các đỉnh (kề) của hình vuông là tam giác
là các đỉnh (kề) của hình vuông là tam giác 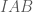 vuông cân tại $laiex I$.
vuông cân tại $laiex I$.





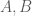 , từ đó suy ra tọa độ của
, từ đó suy ra tọa độ của 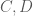 đối xứng lần lượt với
đối xứng lần lượt với 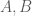 qua
qua 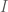 .
.
và
Điều kiện để
Em thử giải hệ này, tìm
Rồi suy ra tọa độ của
ThíchThích
Còn có cách khác: Là em dùng phép quay (góc ) quanh tâm
) quanh tâm 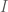
ThíchThích
thay oi cho em hoi truong co blog hoa hoc khong thay nhi?
ThíchThích
Ồ. Có lẽ em phải tìm trên mạng coi thử nhé.
Một số giáo viên Hóa học ở nhiều trường trong nước đã lập blog, em thử tìm nhé !
Ở trường thầy chưa có ! Em thông cảm.
ThíchThích
thay oi, e hay gap kho khan trong cac bai tap ve hinh hoc khong gian. Thay co bi quyet gi giup e khong a. Nhat la ve ca xac dinh goc giua duong thang va mat phang, goc giua 2 mat phang
ThíchThích
A(a,0,0) B(0,b,0) C(0,0,c)
a^2+b^2+c^2=3
tim a,b,c sao cho khoang cach tu goc toa do den (ABC) la lon nhat
ThíchThích
Đầu tiên ta viết phương trình mặt phẳng và tính khoảng cách từ gốc tọa độ đến mặt phẳng
và tính khoảng cách từ gốc tọa độ đến mặt phẳng  .
. tồn tại (có nghĩa) là
tồn tại (có nghĩa) là  và
và  không thẳng hàng. Tức là hai trong ba số
không thẳng hàng. Tức là hai trong ba số 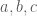 không đồng thời bằng
không đồng thời bằng 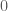 .
. :
: 
 đến mặt phẳng
đến mặt phẳng  là:
là:
 .
.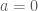 hoặc
hoặc  hoặc
hoặc  thì
thì  đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. lớn nhất chỉ xảy ra khi
lớn nhất chỉ xảy ra khi  .
.
 .
.



 .
. đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng  khi
khi  .
.
 .
.
– Điều kiện để mặt phẳng
– Phương trình mặt phẳng
Khoảng cách từ gốc tọa độ
Trường hợp
DO đó,
Khi đó ta có
Áp dụng bất đẳng thức Cô – si cho ba số dương ta có:
Dấu = xảy ra khi và chỉ khi
Suy ra
Từ đó suy ra
Giải ta được
ThíchThích
Nếu vội vã viết phương trình mặt phẳng theo đoạn chắn:
theo đoạn chắn:

 không ràng buộc
không ràng buộc  nên
nên  chưa xác định.
chưa xác định.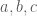 tùy ý nên không phải khi nào cũng viết được
tùy ý nên không phải khi nào cũng viết được  . Ta chỉ dùng phương trình này khi các điểm
. Ta chỉ dùng phương trình này khi các điểm  khác gốc tọa độ .
khác gốc tọa độ . , nếu vội chia tử và mẫu cho
, nếu vội chia tử và mẫu cho  mà không xét xem nó đã khác 0 chưa thì cũng không ổn.
mà không xét xem nó đã khác 0 chưa thì cũng không ổn.
thì dễ mắc nhiều sai lầm và thiếu sót sau:
– điều kiện
Vì
– Trong lúc tính khoảng cách
ThíchThích
ak kho the.
ThíchThích
thay oi giai dum em bai vecto MA=2MB trong do A(2;-3;1) va B(1;-1;4)
ThíchThích
Yêu cầu bài toán là gì vậy em ? Có phải tìm tọa độ điểm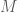 không ?
không ?
ThíchThích