Giải đề số 10
Câu I.2: Xác định
để đường thẳng
cắt đồ thị
tại hai điểm phân biệt
sao cho tiếp tuyến tại
của
song song với nhau.
Gợi ý Giải:
– Tìm đ/k của để
cắt
tại hai điểm phân biệt
– Tính hệ số góc tiếp tuyến của tại hai điểm đó rồi cho chúng bằng nhau.
– Tìm giá trị của thỏa điều kiện.
Lời giải:
* Tập xác định của hàm số .
– Đạo hàm hàm số
* Ph/trình hoành độ giao điểm của và
Xét p/trình có
Mặt khác, thay vào vế trái
ta được
Điều này chứng tỏ không phải là nghiệm của
– Từ đó suy ra, luôn có hai nghiệm phân biệt thỏa
. Tức là
cắt
tại hai điểm phân biệt
với mọi
.
* Gọi lần lượt là hoành độ của
, khi đó
là hai nghiệm của
nên theo định lý Viet ta có
,
– Hệ số góc của tiếp tuyến với tại
là
– Hệ số góc của tiếp tuyến với tại
là
– Theo đề bài, hai tiếp tuyến với tại
song song với nhau nên ta có
– Vì nên ta chỉ có được
Hay
* Kết luận: Giá trị của cần tìm là
Câu II.1: Giải phương trình
PP: P/trình này có dạng tổng quát
– Cách giải: Đặt .
Ta biết , suy ra
và
luôn cùng dấu.
Suy ra
Mà
Suy ra
– Khi đó
Suy ra .
– Ta đưa được PT tổng quát về PT bậc hai theo ẩn số .
Chú ý: nhé !
Giải:
* Điều kiện:
* Đặt , ta có
. Suy ra
.
Ngoài ra,
* P/trình đã cho trở thành
P/trình này có hai nghiệm (thỏa mãn),
(không thỏa mãn).
* Vậy ta có phương trình
Các nghiệm này thỏa mãn điều kiện .
* Vậy phương trình đã cho có các nghiệm cho bởi công thức
Câu II.2:
Giải bất phương trình
Gợi ý giải:
* Điều kiện:
* Với điều kiện trên, ta xét bất phương trình đã cho trên hai khoảng của tập xác định.
+Với , ta có
nên
.So sánh hai vế ta thấy
vô nghiệm.
+ Với , thỏa mãn
nên
là một nghiệm của
.
+ Với , ta có
. Bình phương hai vế của
ta được
Trường hợp này, tập nghiệm của bất phương trình là .
* Kết hợp ba trươgnf hợp đã xét, ta có tập nghiệm của là
Nhận xét:
Có thể trình bày theo dạng tổng quát như sau:
Áp dụng, ta có
—-> Tùy theo khả năng, các bạn hãy chọn cách làm phù hợp và đừng để mất nghiệm, bạn nhé !
Xem tiếp các câu còn lại ở trang tiếp theo

thầy ơi sao em không donwload dược lời giải đề 8 9 10 11
ThíchThích
sao e download de 9 10 11 ma ko dc ha thay?mong thay hay cho vao 1file pdf de de doawload thay a.cam on thay
ThíchThích
xin thay lan sau giai de xin hay cho vao1 file pdf cho tien.chu neu giai tren web khi tai ve de bi that lac file
cam on
ThíchThích
thưa thầy em thấy chổ (1+i)^2009=(1+i)(1+i)2008=(1+i)(2i)^2008 thầy giải bị vô lí theo em phải như thế này mới đúng (1+i)^2009=(1+i)(1+i)^2008=(1+i)(1+i)^2*1004
=(1+i)(2i)^1004
do (1+i)^2=2i
thầy thử xem lại coi phải không ạ?^^ em xin lỗi thầy nếu em nhầm nhé.
ThíchThích
Vâng !

![= \left( {1 + i} \right).\left[ {\left( {1 + i} \right)^2 } \right]^{1004} = \left( {1 + i} \right)\left( {2i} \right)^{1004}](https://s0.wp.com/latex.php?latex=%3D+%5Cleft%28+%7B1+%2B+i%7D+%5Cright%29.%5Cleft%5B+%7B%5Cleft%28+%7B1+%2B+i%7D+%5Cright%29%5E2+%7D+%5Cright%5D%5E%7B1004%7D++%3D+%5Cleft%28+%7B1+%2B+i%7D+%5Cright%29%5Cleft%28+%7B2i%7D+%5Cright%29%5E%7B1004%7D+&bg=ffffff&fg=4e4e4e&s=0&c=20201002)

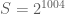 .
.
Cảm ơn em. Đúng phải là
Khi đó
Thầy đã đính chính lại rồi đó em.
Một lần nữa cảm ơn em.
ThíchThích
thua thay thay giai sai rui.theo em![(1+i) ^{2008} =[(1+i)^2]^{1004}=(2I)^{1004}=2^{1004}.i^{1004}](https://s0.wp.com/latex.php?latex=%281%2Bi%29+%5E%7B2008%7D+%3D%5B%281%2Bi%29%5E2%5D%5E%7B1004%7D%3D%282I%29%5E%7B1004%7D%3D2%5E%7B1004%7D.i%5E%7B1004%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) chu.xin loi thay e co ji sai mong thay thong cam nhe.
chu.xin loi thay e co ji sai mong thay thong cam nhe.
ThíchThích
mong thầy trả lời sớm ạ em cảm ơn thầy nhiều
ThíchThích
Thưa thầy,thấy có tểh cho tụi em xin link download lời giải đề số 9,10 dc k ạ
Em cảm ơn thầy
ThíchThích
Thanks
ThíchThích
Sao ko có link download như những đề trước hả thầy
ThíchThích
thầy ơi,bài giải này nếu copy sang word rồi in ra thì hàm và biến,công thức màu nhạt lắm thầy ạ,không đọc được.em chỉnh mãi mà cũng không chỉnh được,có cách nào để sửa được không thầy?
ThíchThích
Cho link down di thay` oi :((
ThíchThích
giúp em bài tìm lim đề 09
ThíchThích
Em xem tại đây
Em chú ý, ở cuối mỗi bài viết có từ 1 đến 3 trang.
Em hãy click vào link để đến các trang đó !
ThíchThích
em khong thay dap an cau 6b dau thay
ThíchThích
Vâng !
Thầy gửi file định hướng + bài giải Câu VI.b – Đề 10 –> để các em tham khảo.
Tải file về máy
Chúc các em học – ôn tập tốt !
ThíchThích
thầy ơi! câu VII.b đề 10 em đọc bài giải mà vẫn chưa hiểu rõ,thấy giải thích kĩ lại giùm em nhe thầy
ThíchThích
Nói chung em cần khai triển hai nhị thức : và
và 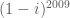 theo công thức Newton.
theo công thức Newton.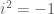 và đặc biệt:
và đặc biệt: 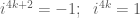 để áp dụng trong hai khai triển trên.
để áp dụng trong hai khai triển trên.
Chú ý rằng
Sau đó cộng hai khai triển theo vế để rút gọn các tổ hợp với chập (chỉ số) lẻ
Em tự thử xem nhé !
ThíchThích
Thầy ơi, giả sử trong phần đặt điều kiện ở câu II1 mà em quên đặt trị tuyệt đối của t>=2 nhưng cuối cùng em vẫn loại nghiệm 2/3 (do vô nghiệm), đi thi làm vậy có bị trừ không hả thầy?
ThíchThích
Khi làm bài, nếu không đặt điều kiện của thì em vẫn tìm được nghiệm
thì em vẫn tìm được nghiệm 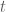 .
.
Sau đó em vẫn giải phương trình thu được nhưng cần kiểm tra lại (thử lại) để loại các nghiệm ngoại lai.
Bài giải vẫn đúng em à và được điểm tối đa.
ThíchThích
thay em tim khong thay dap an cau 6b dau ca thay co the huong dan em cach tai duoc khong?
ThíchThích
Vâng ! Ở đây em nhé. Tải về câu VI.b – Đề 10
ThíchThích
thua thay theo em cau 2 bai VIa thay da tinh nham toa do cua vec to IP. Theo em thay da tinh nham sang vec to PN.mong thay xem lai
ThíchThích
thanks Thầy đã giảng giải cho em bài rất hay!
ThíchThích
Pingback: Giải đề thi đại học của Thầy Đỗ Cao Long «