Toán Blog
Các em học sinh các khối lớp cùng tham gia giải một số bài toán trên blog để luyện tập, và rèn luyện thêm kỹ năng giải toán của mình nhé .
Đầu tiên là một bài toán hay về mặt cầu dành cho học sinh lớp 12, ôn thi ĐH, CĐ
Bài toán 1: Trong không gian Oxyz cho hai mặt cầu có phương trình
Hãy chứng tỏ rằng cắt nhau theo giao tuyến là một đường tròn .
Hãy xác định tâm và tính bán kính của đường tròn giao tuyến đó.

Răng mà ko có đề dành cho lớp 10 thầy? Mà nếu có thì thầy cho dễ dễ á thầy ơi!! hìhì
ThíchThích
Vâng ! Sẽ có cho tất cả các lớp em afh. Em đợi nhé
ThíchThích
mklc
ThíchThích
giai giup pt: sin x + cosx = tan x
ThíchThích
Theo mình có thể giải theo hướng đặt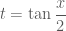 và biểu thị
và biểu thị  ,
,  ,
, 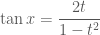
ThíchThích
Thầy ơi
Em học lớp 12
Nên nếu có câu hỏi khó mà ko có liên quan đến các chuyên đề trong phần học toán (như phần hình học ko gian…), muốn thầy giúp đỡ thì phải gửi bài ở đâu ạ.
gửi trong phần này đc ko ạ
mong thầy giúp đỡ
em xin cảm ơn trước.
ThíchThích
Chào em !
Vâng . Hoàn toàn được em à. Rất mong giúp được em một phần nào trong quá trình học toán.
ThíchThích
Thầy ơi giải giúp em bài tích phân này với!
tích phân
Em giải mãi ko ra .
Em xin cám ơn thầy trước.
ThíchThích
Xem phân tích như sau:

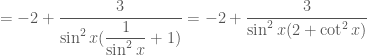
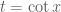 , ta có
, ta có 
Đến đây, đổi biến số bằng cách đặt
EM tự giải tiếp nhé !
ThíchThích
oa …cám ơn thầy nhiều lắm!
Lần sau lại mong thầy giúp đỡ.
ThíchThích
Nhưng thầy ơi
em có thắc mắc về lời giải bài toán trên là nếu rút (sin bình x ) ra thì ở mẫu có (1/sin bình x) mà cận ta có 0 nên em tưởng ko đc rút như thế
ThíchThích
Vâng ! Đúng là có vấn đề như em nói (Khi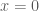 thì
thì  không xác định.
không xác định.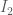 trên đoạn từ
trên đoạn từ  đến
đến  .
.
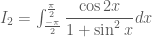
Để khắc phục, em tính tích phân
Hãy chứng minh t/chất đó em nhé !
ThíchThích
Vâng thưa thầy em có biết tính chất đó là tính chất của lớp hàm đặc biệt đúng ko ạ?
Nhưng theo em hiểu thì điều kiện để đc áp dụng tính chất đó là hàm số f(x) cần xét phải là hàm số chẵn (điều đó thì thỏa mãn rồi) và phải liên tục trên đoạn [-a ; a ] .
Với ( I2) có cận từ (-pi/2) đến (pi/2) thì vẫn làm theo cách rút sin bình ở mẫu ra như thầy giải ở đầu có phải ko ạ !. Nhưng cận vẫn chứa số 0 mà thầy , (1/sin bình x) ko xác định đc.
Em vẫn thắc mắc nên mong thầy giải đáp hộ em.
ThíchThích
Em rất giỏi ! đều làm cho
đều làm cho 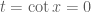 .
.
Đã thấy được tính chất liên tục của hàm số dưới dấu tích phân không được thỏa mãn.
Ngoài ra, nếu để ý thì hai cận
Vậy ta phải khắc phục thế nào nhỉ ?
Em thử tìm xem. Hôm sau thầy sẽ nêu hướng giải.
ThíchThích
Thầy ơi !
Cô em bảo bài này sai đề đó, phải sửa cos2x thành sin2x !
Em vô cùng xin lỗi >…<
cảm ơn thầy đã nhiệt tình giúp đỡ.
ThíchThích
Vẫn giải được em à !
Đợi thầy tìm cách giải nhé ! ,
, 

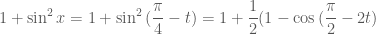
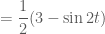 .
. , với
, với  .
.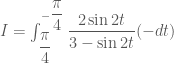
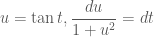

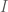 , đổi cận và giải tích phân hàm hữu tỷ thu được xem !
, đổi cận và giải tích phân hàm hữu tỷ thu được xem !
Dùng cách đặt
Khi đó
Và đổi cận:
Lúc này
– Đến đây, đặt
– Còn
Em thử thế vào
ThíchThích
Tiếp theo, ta có:


Em tự giải ha.
ThíchThích
Ta tính

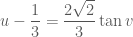 , ta có
, ta có 
 , giả sử
, giả sử 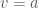
 , giả sử
, giả sử  .
.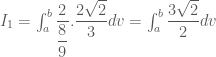
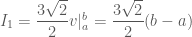
 .
.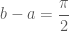
 .
. em tự tính nhé !
em tự tính nhé !
Đặt
Đổi cận: Với
Với
Khi đó
Vậy,
Lại có
Giá trị này không xác định, suy ra
Vậy
CÒn tích phân
ThíchThích
Mà ta nên tính
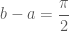 thì hợp lý hơn ! OK ???
thì hợp lý hơn ! OK ???
Suy ra
Trên đây là một hướng giải (hơi dài, khó). Em thử tìm thêm cách khác nhé !
ThíchThích
Lúc đầu em và mấy đứa bạn em cũng giải giống thầy đó.
Nhưng thấy vừa dài lại khá rắc rối cho nên thôi ko làm ra kết quả cuối cùng.
em cám ơn thầy .
Hi vọng lần sau thầy cũn giúp đỡ.
ThíchThích
Thầy ơi bài này khó quá thầy giúp em với
tích phân
Xin thầy giúp em
ThíchThích
Trả lời Anh tú:
Bước 1: Chứng minh .
. .
.
Bắng cách đổi biến
Bước 2: Viết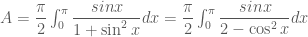 .
.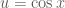 .
.
Rồi đổi biến
Đến đây em tự giải ha.
ThíchThích
Cám ơn thầy trước
ThíchThích
Cám ơn thầy ạ .Thầy ơi những bài này lạ quá không thấy ở trường, cho em hỏi có thi DH hoc không?.Tích phân đa dạng quá.
ThíchThích
thầy ơi em đặt rồi lại không đến bước 2 xin thầy giúp
ThíchThích
Bước 1: Đặt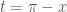 , ta có
, ta có 
 , với
, với  .
.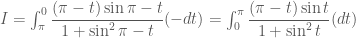 .
.
 (*)
(*)
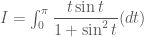 .
.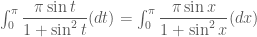
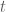 và
và  cho nhau).
cho nhau).
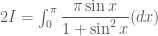 .
. .
.
Đổi cận:
Ta có
Ta biết, giá trị tích phân không phụ thuộc vào đối số nên, ta có:
Còn
(Đổi vai trò của
Thay vào (*), được
Hay
Suy ra
Bước 2: Em tự giải nhé !
ThíchThích
Bài toán Tổng quát: Cho hàm số liên tục trên đoạn
liên tục trên đoạn ![[1;1]](https://s0.wp.com/latex.php?latex=%5B1%3B1%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.
Khi đó
ThíchThích
e thua thay hih nhu la i =tich phan 0>pi pisinx/(1+sin^2x) chu ko phai pi/2
ThíchThích
thầy ơi! giúp em với,thầy cho em xin giáo trình về chức năng và cách sử dụng của phần mềm maple được không thầy!
MOng thầy giúp giùm,cám ơn thầy!
ThíchThích
Em vào trang https://caolong.wordpress.com/tai-nguyen/ để xem nhé. Đầy đủ cả em ạ.
ThíchThích
em hiểu rồi cám ơn thầy bài không biết em sẽ nhờ thầy
ThíchThích
Thầy ơi giải hộ em bài này!
Giải hệ phương trình gồm (1) và (2):
(1) x mũ 3 nhân y = 24
(2) 2 nhân căn bậc ba của x mũ ba – y = 6 căn bậc ba của ba
Cảm ơn thầy trước.
Em thế rổi giải nhưng cách đó ko hay thầy nghĩ xem còn cách nào hay và ngắn hơn hộ em.
ThíchThích
Có phải em hỏi hệ sau không:
![\left\{\begin{array}{l} x^3y=24 \, \, \, (1) \\ 2\sqrt[3]{x^3}-y=6\sqrt[3]{3} \, \, \,(2) \end{array} \right.](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bl%7D+x%5E3y%3D24+%5C%2C+%5C%2C+%5C%2C+%281%29++%5C%5C+2%5Csqrt%5B3%5D%7Bx%5E3%7D-y%3D6%5Csqrt%5B3%5D%7B3%7D+%5C%2C+%5C%2C+%5C%2C%282%29+%5Cend%7Barray%7D+%5Cright.&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
ThíchThích
Chết em nhầm ở (2) thì là căn bậc 2 thôi ạ.
ThíchThích
Thôi em nhắc lại cho đỡ nhầm vậy
(1) giữ nguyên
(2): 2 nhân căn bậc hai của x mũ ba + y = 6 nhân căn bậc ba của ba.
Một lần nữa xin lỗi thầy.
ThíchThích
Vậy, em hỏi hệ sau :
![\left\{\begin{array}{l} x^3y=24 \, \, \, (1) \\ 2\sqrt{x^3}+y=6\sqrt[3]{3} \, \, \,(2) \end{array} \right.](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bl%7D+x%5E3y%3D24+%5C%2C+%5C%2C+%5C%2C+%281%29++%5C%5C+2%5Csqrt%7Bx%5E3%7D%2By%3D6%5Csqrt%5B3%5D%7B3%7D+%5C%2C+%5C%2C+%5C%2C%282%29+%5Cend%7Barray%7D+%5Cright.&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
ThíchThích
Đ/kiện: . Nhưng thấy,
. Nhưng thấy, 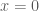 không thỏa mãn hệ.
không thỏa mãn hệ.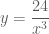 với
với 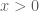 , thế vào (2) ta được:
, thế vào (2) ta được:
![2\sqrt{x^3}+\dfrac{24}{x^3}=6\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=2%5Csqrt%7Bx%5E3%7D%2B%5Cdfrac%7B24%7D%7Bx%5E3%7D%3D6%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.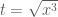 ,
, 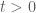 .
.![2t+\dfrac{24}{t^2}=6\sqrt[3]{3} \Leftrightarrow 2t^3+24=6\sqrt[3]{3}t^2](https://s0.wp.com/latex.php?latex=2t%2B%5Cdfrac%7B24%7D%7Bt%5E2%7D%3D6%5Csqrt%5B3%5D%7B3%7D+%5CLeftrightarrow+2t%5E3%2B24%3D6%5Csqrt%5B3%5D%7B3%7Dt%5E2&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![a=\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=a%3D%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) , ta có
, ta có 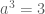 nên
nên  .
.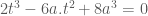
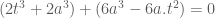

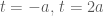
![x=\sqrt[3]{t^2}](https://s0.wp.com/latex.php?latex=x%3D%5Csqrt%5B3%5D%7Bt%5E2%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.
Từ (1), rút
Đặt
Ta có ph/trình
Lại đặt
Ta có phương trình
Dễ dàng nhóm hạng tử theo cách phân tích:
Để đưa về p/trình tích
Giải ta được hai nghiệm
Từ cách đặt ta suy ra
Với![t=-a=-\sqrt[3]{3} <0](https://s0.wp.com/latex.php?latex=t%3D-a%3D-%5Csqrt%5B3%5D%7B3%7D+%3C0&bg=ffffff&fg=4e4e4e&s=0&c=20201002) , nên loại.
, nên loại.
Với![t=2a=2\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=t%3D2a%3D2%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) , ta có
, ta có ![t^2=4a^2=4\sqrt[3]{9}](https://s0.wp.com/latex.php?latex=t%5E2%3D4a%5E2%3D4%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) và
và ![x=\sqrt[3]{4\sqrt[3]{9}}](https://s0.wp.com/latex.php?latex=x%3D%5Csqrt%5B3%5D%7B4%5Csqrt%5B3%5D%7B9%7D%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![y=\dfrac{24}{x^3}=\dfrac{24}{4\sqrt[3]{9}}=\dfrac{6}{\sqrt[3]{9}}=2\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=y%3D%5Cdfrac%7B24%7D%7Bx%5E3%7D%3D%5Cdfrac%7B24%7D%7B4%5Csqrt%5B3%5D%7B9%7D%7D%3D%5Cdfrac%7B6%7D%7B%5Csqrt%5B3%5D%7B9%7D%7D%3D2%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.
và
Kết luận, hệ có một nghiệm![(x=\sqrt[3]{4\sqrt[3]{9}}; y=2\sqrt[3]{3})](https://s0.wp.com/latex.php?latex=%28x%3D%5Csqrt%5B3%5D%7B4%5Csqrt%5B3%5D%7B9%7D%7D%3B+y%3D2%5Csqrt%5B3%5D%7B3%7D%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
ThíchThích
Em thấy ở (2) mình dùng cosi hay hơn ( vì x, y đều >0)
Có đc ko thầy.
ThíchThích
Được chứ em.![2\sqrt{x^3}+y=\sqrt{x^3}+\sqrt{x^3}+y \geq 3\sqrt[3]{\sqrt{x^3}\sqrt{x^3}y}](https://s0.wp.com/latex.php?latex=2%5Csqrt%7Bx%5E3%7D%2By%3D%5Csqrt%7Bx%5E3%7D%2B%5Csqrt%7Bx%5E3%7D%2By+%5Cgeq+3%5Csqrt%5B3%5D%7B%5Csqrt%7Bx%5E3%7D%5Csqrt%7Bx%5E3%7Dy%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![2\sqrt{x^3}+y \geq 3\sqrt[3]{x^3y}](https://s0.wp.com/latex.php?latex=2%5Csqrt%7Bx%5E3%7D%2By+%5Cgeq+3%5Csqrt%5B3%5D%7Bx%5E3y%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.![2\sqrt{x^3}+y \geq 3\sqrt[3]{24}=6\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=2%5Csqrt%7Bx%5E3%7D%2By+%5Cgeq+3%5Csqrt%5B3%5D%7B24%7D%3D6%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.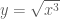 .
.![x^3 \sqrt{x^3}=24 \Leftrightarrow x^3=\sqrt[3]{24^2}=4\sqrt[3]{9}](https://s0.wp.com/latex.php?latex=x%5E3+%5Csqrt%7Bx%5E3%7D%3D24+%5CLeftrightarrow+x%5E3%3D%5Csqrt%5B3%5D%7B24%5E2%7D%3D4%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![x=\sqrt[3]{4\sqrt[3]{9}}](https://s0.wp.com/latex.php?latex=x%3D%5Csqrt%5B3%5D%7B4%5Csqrt%5B3%5D%7B9%7D%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) ;
; ![y=\sqrt{4\sqrt[3]{9}}=2\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=y%3D%5Csqrt%7B4%5Csqrt%5B3%5D%7B9%7D%7D%3D2%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
Nếu sử dụng thành thạo biến đổi Bđt, em ó thể sử dụng nó.
Ta có
Hay
Thay (1) vào, ta được
Vậy dấu “=” xảy ra, tức là ta có
Thay vào (1) được
Suy ra
ThíchThích
thay oi lam ho em bai nay:
tu cac chu so 0,1,2,3,4 hay lap cac so co 5 chu so khac nhau. tinh tong cac so ay
ThíchThích
Lần này lại nhờ thầy giúp đỡ 😀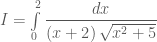
Thầy ơi giải giúp em con tích phân sau đc ko ạ?
tích phân
mong thầy giúp đỡ.
ThíchThích
Em thử đặt , sau đó viết tích phân đã cho về dạng
, sau đó viết tích phân đã cho về dạng

 .
.
Trong đó
Tích phân này em có thể giải theo nhiều cách. Hãy thử làm xem nhé !
ThíchThích
Thầy ơi có cách khác ko ạ?
Cách trên là giải dùng arc tan đúng ko ạ???
Cách này bọn em ko đc học nên em nghĩ ko đc dùng????
Mong thầy giúp:D
ThíchThích
Thầy ơi…….giúp em với…….
ThíchThích
Cái này bạn không cần thiết mà cách của thầy là đúng oài bạn có thể lách đừng nói đến acrtan là được
Good Luck
ThíchThích
giup em bai toan dai so lop 11
ThíchThích
Vâng. Em có thể ghi đề bài và đưa lên nhé !
ThíchThích
Thầy ơi! có thể cho em hướng giải bài toán trên.
ThíchThích
giai gium bai toan : cho tam giac ABC co 3 goc nhon . Chung minh : AB^2 + AC^2 -AB
x AC
ThíchThích
Oh. Em có thể đánh lại đề rõ ràng hơn không.
(Tuần nay, do phải chống bão, lại bị mất điện nên thầy không online được . Mong các em thông cảm)
ThíchThích
Em có vài bài ko biết làm, nhờ thầy chỉ giúp
1.Trong khai triển (2x – y^2)^33 tìm số hạng mà lũy thừa của x và của y có số mũ giống nhau
2. Có bao nhiêu số tự nhiên gồm 3 chữ số khác nhau và khác 0, biết tổng của 3 chữ số này bằng 8
3. Tìm số hạng thứ 4 trong khai triển (8a^3 – 1/2 x^2)^6 theo lũy thừa tăng dần của x
ThíchThích
Câu 1. Có thể trình bày cách giải như sau có dạng
có dạng

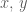 bằng nhau, ta có
bằng nhau, ta có 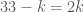

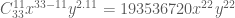
Các số hạng trong khai triển biểu thức
Theo yêu cầu bài toán (số mũ của
Kết luận: Số hạng cần tìm là
ThíchThích
Câu 2: Gọi số cần tìm có dạng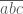
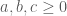 và
và  nên
nên 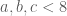
 và
và 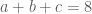 , khi đó ta có các trường hợp sau:
, khi đó ta có các trường hợp sau: : Có
: Có 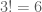 số thỏa ycbt.
số thỏa ycbt.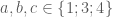 : Có
: Có 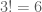 số thỏa ycbt.
số thỏa ycbt. số tự nhiên thỏa ycbt.
số tự nhiên thỏa ycbt.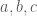 có đúng một chữ số bằng
có đúng một chữ số bằng 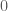 và
và 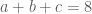 , ta có các trường hợp sau:
, ta có các trường hợp sau: : Có
: Có  số thỏa ycbt.
số thỏa ycbt.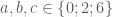 : Có
: Có  số thỏa ycbt.
số thỏa ycbt. : Có
: Có  số thỏa ycbt.
số thỏa ycbt. số tự nhiên thỏa ycbt.
số tự nhiên thỏa ycbt.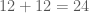 số tưn nhiên thỏa ycbt.
số tưn nhiên thỏa ycbt.
* do
Ta sẽ chia bai toán ra hai trường hợp:
TH1: Cả ba chữ số
–
–
Trường hợp này có
TH2: Trong 3 chữ số
–
–
–
Trường hợp này có
Tóm lại: Có tất cả
ThíchThích
Câu 3: Tìm số hạng thứ 4 trong khai triển theo lũy thừa tăng dần của
theo lũy thừa tăng dần của 
 có dạng
có dạng
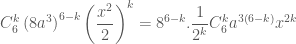
 ta sẽ được các số hạng thứ nhất, thứ hai, thứ ba, thứ tư, thứ năm ,… theo lũy thừa tăng dần của
ta sẽ được các số hạng thứ nhất, thứ hai, thứ ba, thứ tư, thứ năm ,… theo lũy thừa tăng dần của  .
. theo lũy thừa tăng dần của
theo lũy thừa tăng dần của  là số hạng chứa
là số hạng chứa  ,
,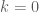 , ta có số hạng thứ nhất :
, ta có số hạng thứ nhất : 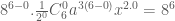
 theo lũy thừa tăng dần của
theo lũy thừa tăng dần của  là số hạng ứng với
là số hạng ứng với  .
.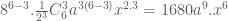
—
Các số hạng trong khai triển biểu thức
Cho
Như vậy số hạng thứ nhất trong khai triển biểu thức
Tức là cho
Số hạng thứ tư trong khai triển biểu thức
Số hạng đó là:
ThíchThích
Thầy ơi!!!
Em học toán Hình Học 11CB tới Chương II “đường thẳng và mặt phẳng trong không gian. quan hệ song song” nhưng em hok biết giải bài tập không biết cẽ hình luôn. Thầy làm ơn uploand bài huớng dẫn giải các bài tập của chương đó và cách vẽ hình luôn nha Thầy . Cảm ơn!!!
ThíchThích
Vâng !
Thầy sẽ viết kỹ và cỉ dẫn rõ ràng một số dạng cơ bản giúp em có thể tự học dạng toán khó này !
ThíchThích
vxxxxxc
ThíchThích
ko co lop 11 a?
ThíchThích
em chào thầy,thầy ơi thầy có thể cho em hỏi 2 bài sau không ạ ,em mât cả tuần mà không ra ạ :
bài 1: giải phương trình sinx+sin2x+sin3x=2;
bài 2: tính nguyên hàm của cos^5(x).căn(x+1)
em cảm ơn thầy ,
ThíchThích
co aj zup e giai baj nay zoi : tap hop cac phan tu ko dem duoc .
A=”3k+1″ . B=”6l+2″
chug mjh rag b la con cua A
ThíchThích
Nếu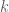 là số nguyên, thì có 2 khả năng:
là số nguyên, thì có 2 khả năng:
Khả năng 1: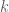 là số nguyên chẵn hoặc bằng
là số nguyên chẵn hoặc bằng 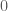 , tức là
, tức là 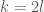 , với
, với  .
. .
.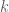 là số nguyên lẻ, tức là
là số nguyên lẻ, tức là 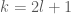 , với
, với  .
. .
.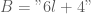 là con của tập
là con của tập 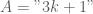 , với
, với  .
.
Lúc đó:
Khả năng 2:
Lúc đó:
Vậy, tập
DO đó, yêu cầu bài toán em hỏi có vấn đề. , ta cho
, ta cho 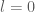 , ta có phần tử
, ta có phần tử  , nhưng trong tập
, nhưng trong tập 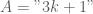 không có phần tử này (tức là không có giá trị nào của
không có phần tử này (tức là không có giá trị nào của 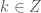 để
để  .
.
Ví dụ, trong
Em xem lại đề bài !
ThíchThích
giúp cho em bài này nhé thầy
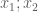 thỏa hệ thức
thỏa hệ thức 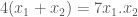
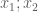
Cho phương trình
a/ Tìm m sao cho phương trình có hai nghiêm
b/ Viết phương trình bậc hai có hai nghiệm là y1 = và y2 =
c/ Tìm hệ thức độc lập đối với m giữa các nghiệm
ThíchThích
Xét phương trình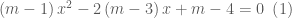
Câu a: có 2 nghiệm phân biệt là
có 2 nghiệm phân biệt là


 thì (1) có 2 nghiệm phân biệt
thì (1) có 2 nghiệm phân biệt  .
.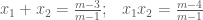
 khi và chỉ khi
khi và chỉ khi 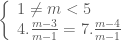


 thỏa yêu cầu bài toán.
thỏa yêu cầu bài toán.
Điều kiện để phương trình
Với điều kiện
Theo định lý Viet ta có:
Từ đó suy ra, (1) có 2 nghiệm phân biệt thỏa điều kiện
Vậy, không có giá trị của
ThíchThích
Câu c: thì (1) có 2 nghiệm phân biệt
thì (1) có 2 nghiệm phân biệt 
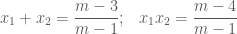 .
.


 (vì cùng bằng
(vì cùng bằng  )
)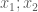 là:
là:


Theo kết quả câu a, với điều kiện
Và theo định lý Viet ta có:
Ta viết lại:
Suy ra:
Vậy, hệ thức liên quan độc lập giữa
ThíchThích
Còn câu b.
Em hãy viết lại đề bài rõ ràng để thầy xem nhé !
ThíchThích
: Giải phương trình:
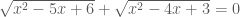
a/
b/
ThíchThích
*Phương trình này có dạng:
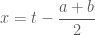
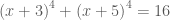 (1)
(1)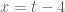 thì phương trình (1) trở thành:
thì phương trình (1) trở thành:
 (2)
(2)
 (3)
(3)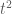 và giải ta được hai nghiệm:
và giải ta được hai nghiệm:
 và
và  (loại).
(loại).
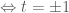
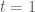 ta có
ta có 
 ta có
ta có 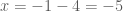 .
.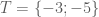
Cách giải là: Đặt
* Áp dụng vào phương trình
Ta đặt
Khải triển vế trái và rút gọn (2), ta được phương trình:
Xem (3) là phương trình bậc hai theo
* Với
Với
Kết luận: Tập nghiệm của phương trình (1) là
ThíchThích
Câu b:
Nhắc lại: Nếu tam thức có 2 nghiệm
có 2 nghiệm  thì ta phân tích được
thì ta phân tích được 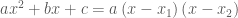
Để ý: Tam thức có hai nghiệm
có hai nghiệm  nên ta phân tích được
nên ta phân tích được 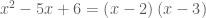
 có hai nghiệm
có hai nghiệm  nên ta phân tích được
nên ta phân tích được  .
.
Tam thức
*Do đó, ta có :
 (1)
(1)
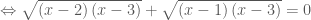 (2)
(2)

![\Leftrightarrow \left\{ \begin{array}{l} x \in \left( { - \infty ;2} \right] \cup \left[ {3; + \infty } \right) \\ x \in \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right) \\ \end{array} \right.](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%5Cleft%5C%7B+%5Cbegin%7Barray%7D%7Bl%7D++x+%5Cin+%5Cleft%28+%7B+-+%5Cinfty+%3B2%7D+%5Cright%5D+%5Ccup+%5Cleft%5B+%7B3%3B+%2B+%5Cinfty+%7D+%5Cright%29+%5C%5C+++x+%5Cin+%5Cleft%28+%7B+-+%5Cinfty+%3B1%7D+%5Cright%5D+%5Ccup+%5Cleft%5B+%7B3%3B+%2B+%5Cinfty+%7D+%5Cright%29+%5C%5C+++%5Cend%7Barray%7D+%5Cright.&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![\Leftrightarrow x \in \left( { - \infty ;2} \right] \cup \left[ {3; + \infty } \right)](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+x+%5Cin+%5Cleft%28+%7B+-+%5Cinfty+%3B2%7D+%5Cright%5D+%5Ccup+%5Cleft%5B+%7B3%3B+%2B+%5Cinfty+%7D+%5Cright%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
*Điều kiện xác định của phương trình (1) và (2) là:
* Bây giờ ta dùng phương pháp chia khoảng để giải phương trình (2)
Trường hợp 1:
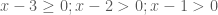 nên ta viết được (2) như sau:
nên ta viết được (2) như sau:
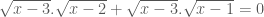
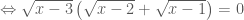 (2a)
(2a) nên
nên  , do đó ta có
, do đó ta có
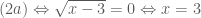

Ta có
Vì
Trường hợp này phương trình (2) có một nghiệm
ThíchThích
Trường hợp 2:![x \in \left( { - \infty ;2} \right]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5Cleft%28+%7B+-+%5Cinfty+%3B2%7D+%5Cright%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
Em thử lập luận và giải tương tự nhé !
Chú ý:
Để giải (2) các em có thể dùng phương pháp “xét dấu vế trái” để viết lời giải gọn hơn và nhanh hơn !
ThíchThích
Chứng minh với mọi a, b, ta có: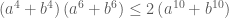
ThíchThích
Đặt
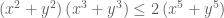



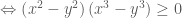

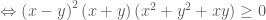
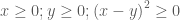 .
.
Bất đẳng thức đã cho viết lại dạng:
Đẳng thức này luôn đúng, vì
ThíchThích
ThíchThích
Cho tam giác ABC nội tiếp trong đường tròn tâm O. Ba đường phân giác trong của các góc A, B, C kéo dài lần lượt cắt đường tròn ngoại tiếp tam giác ABC tại A1, B1, C1. Đường tròn nội tiếp tâm I tiếp xúc với 3 cạnh BC, AC, AB tại A2; B2, C2.
1/ Chứng minh rằng: vecto OI=OA1+OB2+OC2
2/ H là trực tâm tam giác A2B2C2. Chứng minh rằng: O, I, H thẳng hàng.
ThíchThích
thay giup e giai may bai toan lop 10 nay nha kho qua thay oi em rat cam on
ThíchThích
thay neu e muon thay jup may bai toan kho’ thi e phai lam nhu the nao` ak
ThíchThích
Em hãy gửi trực tiếp đề bài qua phản hồi trên blog này. Nếu giúp được thầy sẵn sàng giúp em.
Chúc em học tốt.
ThíchThích
trang web của thầy em thấy rất là hữu ích cám ơn thầy đã tạo ra website này
ThíchThích
Thầy ơi giả cho em bài này:
1.giai he pt: a)x+y+1/x+1/y=4 va x^2+y^2+1/x^2+1/y^2=4
b)x^4+y^4=1 va x^6+y^6=1
2.cho he pt: x+xy+y=m+1 va x^2y+xy^2=m.tim m de he co it nhat 1 nghiem thoa man:x.>0,y>o
ThíchThích
Em nhờ thầy chỉ dùm em bài này:
Trong mặt phằng tọa độ Oxy lập pt tổng quát của đường thẳng delta co hệ số góc -3/4 , và tạo với các trục tọa độ 1tam giác có diện tích 24 .
ThíchThích
Đường thẳng có hệ số góc bằng
có hệ số góc bằng  có phương trình dạng:
có phương trình dạng:  , trong đó
, trong đó  .
. cắt trục
cắt trục  tại
tại 
 cắt trục
cắt trục 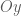 tại
tại  .
. ( tam giác do
( tam giác do  tạo với hai trục tọa độ tạo thành) bằng:
tạo với hai trục tọa độ tạo thành) bằng:
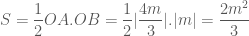 .
.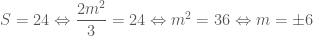 .
.
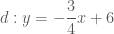 và
và 
Lúc đó,
và
Diện tích của tam giác
Theo đề cho ta có :
Vậy, có hai đường thẳng thỏa mãn yêu cầu bài toán có phương trình:
ThíchThích
Thầy ơi, giải giúp em bài này nha, em cảm ơn thầy rất nhiều
Trong không gian tọa độ Oxyz, cho điểm A(2;0;0), C(0;4;0), S(0;0;4). Tìm tọa độ điểm B thuộc mặt phẳng Oxy sao cho tứ giác OABC là hình chữ nhật. Viết phương trình mặt cầu đi qua 4 điểm O,B,C,S.
ThíchThích
Ý 1: Chứng minh tứ giác là hình chữ nhật .
là hình chữ nhật .
Nhận xét: điểm suy ra tam giác
suy ra tam giác  vuông tại
vuông tại  .
. .
. là hình chữ nhật là
là hình chữ nhật là  là hình bình hành (vì đã có
là hình bình hành (vì đã có  )
)


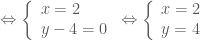
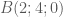
Gọi tọa độ điểm
Điều kiện để tứ giác
Vậy tọa độ điểm
Ý 2: Viết phương trình mặt cầu đi qua bốn điểm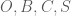 .
. nên tam giác
nên tam giác 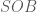 vuông tại
vuông tại  .
. nên
nên  vuông tại
vuông tại  .
.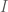 là trung điểm của cạnh
là trung điểm của cạnh 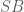 , ta có
, ta có 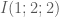 .
.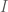 là trung điểm của cạnh huyền
là trung điểm của cạnh huyền 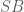 của các tam giác vuông
của các tam giác vuông 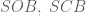 nên suy ra
nên suy ra 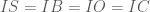 .
.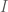 là tâm của mặt cầu đi qua 4 điểm
là tâm của mặt cầu đi qua 4 điểm 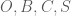 .
.
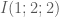 và bán kính
và bán kính  ):
):

Nhận xét: điểm
Dễ chứng minh được
Gọi
Vì
Vậy
Bán kính mặt cầu:
Suy ra phương trình mặt cầu cần tìm (có tâm
— là tâm mặt cầu đi qua bốn điểm
là tâm mặt cầu đi qua bốn điểm  .
.
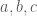 suy ra tọa độ của
suy ra tọa độ của 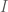 .
.
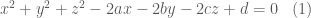
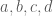 là các số thực thỏa điều kiện
là các số thực thỏa điều kiện 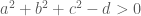 )
) nên tọa độ các điểm này thỏa mãn phương trình
nên tọa độ các điểm này thỏa mãn phương trình  .
. vào phương trình
vào phương trình  ta sẽ có hệ gồm bốn phương trình.
ta sẽ có hệ gồm bốn phương trình. .
. , bán kính mặt cầu
, bán kính mặt cầu 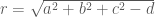 .
.
EM có thể xác định tâm mặt cầu bằng các cách khác:
Chẳng hạn:
Cách 1:
Gọi
Ta có:
Giải hệ này ta tìm được
—
Cách 2:
Giả sử phương trình mặt cầu cần tìm có dạng:
(với
Vì mặt cầu đi qua 4 điểm
Thay tọa độ 4 điểm
Giải hệ này tìm được
Suy ra phương trình mặt cầu.
Ngoài ra ta có tâm mặt cầu:
ThíchThích
Cảm ơn thầy rất…rất nhiều.
Ý 2, em tìm H(1;2;0) là trung điểm OB. H là tâm đường tròn ngoại tiếp tam giác OCB. Đường thẳng vuông góc vs (OCB) tại H cắt mp trung trực của đoạn OS tại I => I là tâm mặt cầu đi qua 4 điểm O,B,C,S => I(1;2;2); R = OI = 3 => pt mc cần tìm.
Cách này có được hok thầy, trong lớp có mỗi em la giải theo cách đó. Lớp em mới kiểm tra 1 tiết bài đó.
Cảm ơn thầy. Mong thầy giúp đỡ em nhiều thêm.
ThíchThích
Em làm theo cách đó đúng rồi.
(EM đã sử dụng các bước xác định tâm của hình chóp, lăng trụ nên lời giải không sai chỗ nào. Em làm rất tốt)
ThíchThích
Dạ, em cảm ơn thầy nhiều!
Thầy giải giúp em bài này với:
Cho 9 số thực bất kì a1, b1, c1, a2, b2, c2, a3, b3, c3 thỏa mãn:
a1+a2+a3=3; b1+b2+b3=4; c1+c2+c3=12
cm: sqrt(a1+b1+c1) + sqrt(a2+b2+c2) + sqrt(a3+b3+c3 ) >= 13
Gần thi đại học rồi mà em vẫn còn phần tổ hợp, chỉnh hợp, hoán vị của lớp 11 và phần bất đẳng thức chưa ôn, thầy có tài liệu nào không cho em xin với.
Em cảm ơn!
ThíchThích
Tài liệu ôn thi hiện nay trên mạng internet cũng khá nhiều và có một số tài liệu hay.
Thầy chưa viết tài liệu LTĐH, chủ yếu là bài viết cho học sinh yếu, trung bình.
Có gì muốn trao đổi em có thể hỏi. Nếu thầy tìm thấy tài liệu hay thầy sẽ send link cho em.
ThíchThích
Thứ 7 và Chủ Nhật này thầy về quê thăm bố mẹ.
Hẹn trao đổi lại với các em vào tuần sau nhé ! Các em thông cảm.
ThíchThích
Em xem có phải đề bài là: thỏa mãn
thỏa mãn 
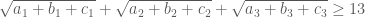
Cho 9 số thực
Chứng minh rằng:
ThíchThích
chao thay!thay oi!giup em giai bai toan phuong trinh nay nha thay.
x+2can(7-x) = 2can(7-x )+can(-x^2 +8x -7) + 1.em cam on thay.
ThíchThích
Có phải phương trình: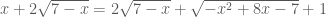 không em. EM kiểm tra lại đề xem.
không em. EM kiểm tra lại đề xem.
ThíchThích
da phai!co bai giai he nay,thay huong dan giup em :
x+y +x^2+y^2=2
x^2+x-y^2-y=0
em xin cam on
ThíchThích
Giải phương trình: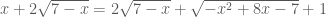 .
.
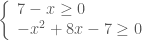

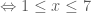
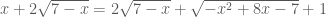

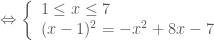




—-
* Điều kiện của phương trình:
* Khi đó, rút gọn 2 số hạng bằng nhau ở hai vế ta có:
* Vậy, phương trình đã cho có hai nghiệm:
ThíchThích
Giải hệ:
 .
.
 .
.
 .
. thay vào phương trình đầu của hệ ta được:
thay vào phương trình đầu của hệ ta được:


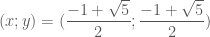 ;
;

 , kết hợp với phươgn trình đầu của hệ đã cho ta có hệ:
, kết hợp với phươgn trình đầu của hệ đã cho ta có hệ:
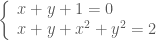
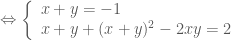
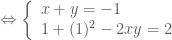

 hoặc
hoặc 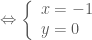 .
. và
và 
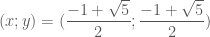 ;
;
 ;
;
 và
và  .
.
——–
Ở phương trình thứ hai của hệ, em biến đổi thành tích như sau:
* Trường hợp
Trường hợp này hệ đã cho có hai nghiệm:
* Trường hợp
Trường hợp này hệ đã cho có hai nghiệm:
* Tóm lại, hệ đã cho có bốn nghiệm:
ThíchThích
Dạ đúng là cái đề đó, thầy giải giúp em nha. Ah`, làm sao để gõ được mấy kí tự như dấu căn ở chỗ gởi phản hồi vậy thầy.
Em cảm ơn.
ThíchThích
Em kiểm tra lại đề lần nữa đi. thỏa mãn giả thiết.
thỏa mãn giả thiết.


Thầy thử thấy đề sai.
Chẳng hạn, cho
Tuy nhiên
ThíchThích
thay oi !thay giai 2 bai ma em gui, thay giup em nha.tai em can gap lam a.em xin cam on thay rat nhieu.:)hihi
ThíchThích
Thầy giải rồi. EM lên xem tham khảo nhé !
ThíchThích
da em cam on ! ma thay oi ,bai dau em gui lon de,cai de la nhu vay ne`:
x+2can(7-x)=2can(x-1)+can(-x^2+8x-7) +1.
em giai ma khong ra.thay giup em nha thay.sang mai em kiem tra roi.cam on thay nhieu:)
ThíchThích
Giải phương trình: .
.

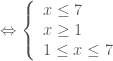
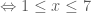



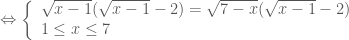

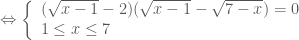

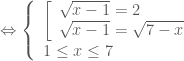



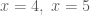 .
. , ta có
, ta có 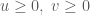
 và
và  . Suy ra
. Suy ra  .
.

* Điều kiện của phương trình:
—-
* Ta có:
Vậy phương trình đã cho có hai nghiệm:
—
Cách khác:
Đặt
Suy ra:
Từ đó, phương trình đã cho trở thành hệ:
Em hãy thử giải hệ này xem nhé !
ThíchThích
thầy giải bài này hay quá , em nhìn hoài mà ko ra luôn
ThíchThích
thầy ơi! giúp em giải bt này ah.
![\dfrac{\log{\sqrt{x+1}+1}} {\log{\sqrt[3]{x-40}}}](https://s0.wp.com/latex.php?latex=%5Cdfrac%7B%5Clog%7B%5Csqrt%7Bx%2B1%7D%2B1%7D%7D+%7B%5Clog%7B%5Csqrt%5B3%5D%7Bx-40%7D%7D%7D&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
lg [căn (x+1) cộng cho 1] chia cho [ lg căn bậc 3 của (x-40).]
em cám ơn thây nhiêu mong thây giúp em. em dang cần gấp.
ThíchThích
Yêu cầu là làm gì vậy em ?
ThíchThích
thay oi.lop em co moi cho bai he phuong trinh nay,ma em giai khong ra ,thay giai giup em nha
x^3-8x =y^3+2y
x^3-3 =3(y^2+1)
ThíchThích
thay oi !giai giup em bai he nay nha.
x^3-8x=y^3+2y
x^3-3=3(y^2+1)
ThíchThích
Giải hệ:
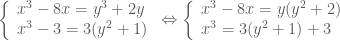

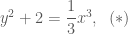 , thay vào phương trình đầu của hệ ta được:
, thay vào phương trình đầu của hệ ta được:
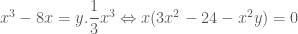
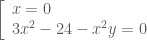
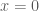 không thỏa mãn
không thỏa mãn  .
.

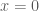 không thõa mãn
không thõa mãn 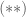 nên ta có
nên ta có 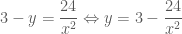 .
. ta được:
ta được: 
————
Từ phương trình thứ hai của hệ này ta có
Vì
Thay vào
ThíchThích
cam on thay
ThíchThích
thay oi!cai cho thay vao (*) ta duoc :(3-(24/x^2)^2)+2=1/3 x^3
(dong` cuoi cung do’ thay) roi minh tiep tuc giai ,sao em ra mu~ lon lam.khong ra duoc.thay huong dan em nha.cam on thay
ThíchThích
Phương trình này sau khi khai triển và quy đồng thì đến bậc 7 và chỉ có 1 nghiệm duy nhất (vô tỷ).
Có thể dùng máy tính để tìm giá trị gần đúng của nghiệm này.
Để thầy tìm cách giải nó xem sao. Nếu không giải được có lẻ phải giải hệ theo hướng khác.
ThíchThích
thay oi,neu nguoi ta cho phuong trinh duong tron (C):x^2+y^2-4x-6y-12=0
a)CMR :diem A(7,-7) nam ngoai duong tron (C)
minh phai lam sao thay.thay giai giup em nha.cam on thay
ThíchThích
– Em xác định tọa độ tâm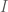 của đường tròn.
của đường tròn. của đường tròn.
của đường tròn.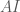 .
.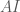 và
và  .
.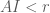 thì điểm
thì điểm  nằm ở trong đường tròn.
nằm ở trong đường tròn. thì điểm
thì điểm  nằm ở ngoài đường tròn.
nằm ở ngoài đường tròn. thì điểm
thì điểm  nằm ở trên đường tròn.
nằm ở trên đường tròn.
– Tính bán kính
– Tính độ dài đoạn
So sánh
-Nếu
-Nếu
-Nếu
———
Em tự tính nhé !
ThíchThích
thay oi,bai nay giai sao thay
cho duong tron (C): x^2+y^2-2my+m^2+4=0
a)dinh m de tu A(2,3) co 2 tiep tuyen den (C)
b)viet phuong trinh tiep tuyen cua duong tron (C) do khi m=6
hihi.cam on thay.
ThíchThích
thay oi co the giup e giai 1 bai tap toan hinh dc hem thay?
ThíchThích
thay oi giai dum e giup bai toan hinh nha thay?
ThíchThích
ai giai giup dum bai toang nay cam on: cho hinh vuong ABCD co tam I(4;-1) va phuong trinh canh AB : x+2y-1=0 . Hay lap phuong trinh hai duong cheo cua hinh vuong. giai giup minh cam on!
ThíchThích
Nhận xét: Hai đường chéo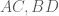 của hình vuông
của hình vuông 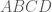 vuông góc với nhau tại
vuông góc với nhau tại 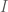 và
và 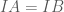
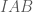 vuông cân tại
vuông cân tại 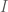 , do đó góc giữa hai đường chéo của hình vuông với đường thẳng
, do đó góc giữa hai đường chéo của hình vuông với đường thẳng  bằng
bằng 
 đi qua
đi qua 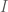 và góc giữa
và góc giữa  và đường thẳng
và đường thẳng  bằng
bằng  .
. và song song với trục
và song song với trục 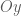 có phương trình
có phương trình  tạo với đường thẳng
tạo với đường thẳng 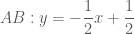 một góc khác
một góc khác  nên không thể là đường chéo hình vuông.
nên không thể là đường chéo hình vuông. và có hệ số góc
và có hệ số góc 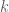 và có phương trình dạng:
và có phương trình dạng:  đồng thời góc giữa
đồng thời góc giữa  và đường thẳng
và đường thẳng  bằng
bằng  .
. có vectơ pháp tuyến
có vectơ pháp tuyến 
 có vectơ pháp tuyến
có vectơ pháp tuyến 
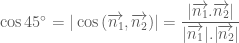


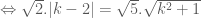 (vì
(vì  )
)


 và
và 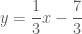
Tức là tam giác
Dựa vào nhận xét trên ta có hướng giải bài toán như sau: Viết phương trình đường thẳng
—————————
Cách 1:
Nhận xét: Đường thẳng qua
Từ đó suy ra, đường chéo hình vuông đi qua
Đường thẳng
Đường thẳng
Ta có
Vậy phương trình hai đường chéo cần tìm của hình vuông là:
ThíchThích
Cách 2: Tìm tọa độ điểm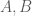 .
.
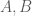 là
là 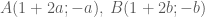 với
với 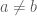 .
. .
.
 là tâm hình vuông nên
là tâm hình vuông nên 
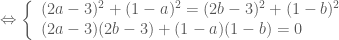

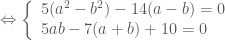
![\Leftrightarrow \left \{ \begin{array}{l} (a-b)[5(a+b)-14]=0 \\ 5ab-7(a+b)+10 = 0 \end{array} \right.](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%5Cleft+%5C%7B+%5Cbegin%7Barray%7D%7Bl%7D+%28a-b%29%5B5%28a%2Bb%29-14%5D%3D0+%5C%5C+5ab-7%28a%2Bb%29%2B10+%3D+0+%5Cend%7Barray%7D+%5Cright.&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
 . (vì
. (vì 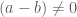 )
)
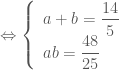
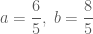 (vì ta đã gỉ sử
(vì ta đã gỉ sử  )
)
————
Phương trình tham số của đường thẳng
Từ đó, gọi tọa độ của
Giả sử
Ta có
Giải hệ này ta được
ThíchThích
thay oi,em co may bai chung minh dang thuc kho wa’,thay giai giup em nha.
1)(sinx+cosx-1)/(sinx-cosx+1)=cosx/(1+sinx)
2)sinx+cosx=(can2) sin(x+(bi/4))=(can2) cos (x-(bi/4))
3)(1-cosx) (1+cot^2x)=4cotx/sinx
4)(1+cosx) /(1-cosx) -(1-cosx)/(1+cosx) =4cotx/sinx
thay oi,co cach nao lam may bai nay de dang khong thay.thay huong dan cach lam cho em cung duoc. em cam on
ThíchThích
Với điều kiện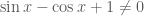 và
và  ta có:
ta có:

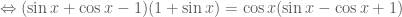


 (đẳng thức này đúng).
(đẳng thức này đúng).
Vậy đẳng thức (ban đầu) cần chứng minh đúng (với điều kiện đã nêu).
ThíchThích
Chú ý công thức cộng:
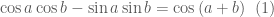

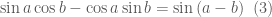


 (theo công thức số
(theo công thức số 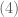 )
)

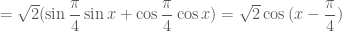 (theo công thức số
(theo công thức số  )
)
—————-
Ta có cách giải câu 2 như sau:
Ý 2:
ThíchThích
Còn có các cách khác.
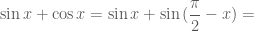
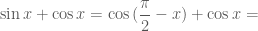
Chẳng hạn dùng công thức biến đổi tổng thành tích và biến đổi.
hoặc
ThíchThích
Đẳng thức ở câu số 3 không đúng.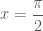 thì hai vế không bằng nhau.
thì hai vế không bằng nhau.
Chẳng hạn với
Em kiểm tra lại đề bài.
ThíchThích
minh mun dang 1 bai len va mun ban giai ho thi lam the nao
ThíchThích
minh mun dang 1 bai toan len va mun duoc ca ban giai ho thi lam the nao
ThíchThích
Em chỉ cần viết đề bài toán trong ô “Gửi phản hồi” ở cuối mỗi trang.
ThíchThích
thay oi bai 3 nek :
3)(1-cosx) (1+cot^2x)=1/(1+cosx)
4)(1+cosx)/(1-cosx) – (1-cosx)/(1+cosx) =4cotx/sinx
5)1- ((sin^2x)/(1+cotx)) -(cos^2x/1+tanx)=sinx.cosx
ma thay oi em con may bai nua,cung kho.thay giup em duoc khong?
ThíchThích
Câu 3:
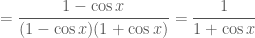
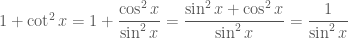
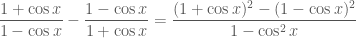

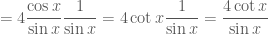

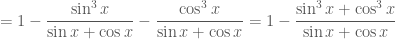


Ta có
Chú ý:
————————-
Câu 4:
————————-
Câu 5:
ThíchThích
thay oi.bai hinh nay giai sao vay thay
1)cho duong tron (c):(x-1)^2+y^2=1 co tam I .tim M thuoc (C) sao cho goc’ IMO =30 do .
2)cho duong tron (C) (x-4)^2+y^2=4 va E(4,1)itim M tren truc tung sao cho tu M ke~ duoc 2 tiep tuyen MA,MB den C voi A ,B la tiep diem va duong thang AB qua E
ThíchThích
Câu 1: có tâm
có tâm 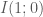 .
.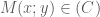 ta có
ta có 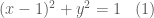 .
. nên ta có
nên ta có 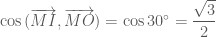

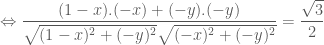

 vào
vào  ta có:
ta có:
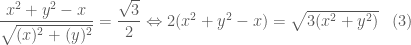
 thay vào
thay vào  ta được:
ta được:
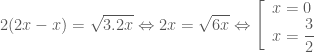
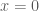 thay vào
thay vào  ta được
ta được  . Trường hợp này ta có
. Trường hợp này ta có 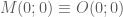 nên loại.
nên loại.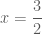 thay vào
thay vào  ta được
ta được  . Trường hợp này ta có hai điểm thỏa yêu cầu bài toán là:
. Trường hợp này ta có hai điểm thỏa yêu cầu bài toán là: 
Đường tròn
Gọi tọa độ của
Theo giả thiết
Thay
Ta có
Với
Với
ThíchThích
thay oi,em gui lai bai 3 roi,thay giai giup em nha.mai em kiem tra roi.cam on thay nhieu !!
ThíchThích
thay oi,con bai 2 nua~!:)thay huong dan em giai nha.cam on thay
ThíchThích
OK!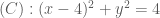 có tâm
có tâm  và bán kính
và bán kính 
 là điểm cần tìm.
là điểm cần tìm. có đường kính
có đường kính 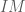 khi đó
khi đó 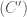 có tâm
có tâm  và bán kính
và bán kính  .
.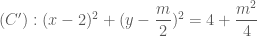
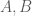 của
của 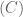 và
và 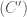 chính là các tiếp điểm của tiếp tuyến với đường tròn
chính là các tiếp điểm của tiếp tuyến với đường tròn 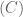 và đi qua điểm
và đi qua điểm  và là nghiệm của hệ:
và là nghiệm của hệ:

 cho
cho  theo vế sau đó rút gọn ta được:
theo vế sau đó rút gọn ta được: 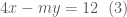
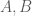 thỏa mãn phương trình
thỏa mãn phương trình  nên
nên 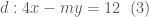 chính là đường thẳng đi qua hai điểm
chính là đường thẳng đi qua hai điểm 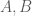 .
.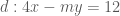 đi qua
đi qua 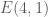 nên ta có:
nên ta có:
 .
.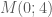 là điểm cần tìm.
là điểm cần tìm.
————–
Đường tròn
Gọi
Xét đường tròn
Phương trình của
Tọa độ giao điểm
Khai triển và trừ theo vế phương trình
Như vậy tọa độ các điểm
Theo giả thiết
Kết luận:
————–
ThíchThích
thay oi!em cung co may bai dang thuc nay ma em khong giai duoc ,thay giup em nha:
1)sin^4x+cos^4x=1-2sin^2xcos^2x
2)sin825độ cos(-2535độ)+cos75độ sin(-555độ)+tan(695độ) tan(245độ)=0
3)sin (x +(85bi/2))+cos (207bi+x)+sin^2(33bi+x) + sin^2(x-(3bi/2))=1
4)(tan^2x -tan^2y) / (tan^2x tan^2y) =(sin^2x-sin^2y) / (sin^2x sin^2y)
ThíchThích
Câu 1:
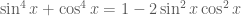

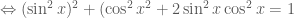

Đẳng thức cuối cùng luôn đúng suy ra đẳng thức đã cho đúng.
ThíchThích
thay oi!giup em may bai nay nha thay :
don gian cac bieu thuc sau :
1)H=cos(15bi-a)+sin(a-(7bi/2))-tan((3bi/2)+a).cot((3bi/2)-a)
2)j=sin(bi+a)+sin(2bi+a)+sin(3bi+a)+…..+sin(100bi+a)
3)L=(tan((19bi/2)-x).cos(36bi-x).sin(x-5bi))/(sin((9bi/2)-x).cos(x-99bi))
4)K=cos(1710do-x)-2sin(x-2250do)+cos(x+900do)+2sin(720do-x)+cos(540do-x)
5)M =(1/tan368do)+((2sin2550do.cos(-188do))/(2cos638do+cos98do))
mong thay huong dan giup em.cam on thay!
ThíchThích
Thay oi thay giai dum e bai nay voi duoc ko ak.
tinh dao ham ham so sau
y=mx^3/3+(m-1)x^2+2mx+m^2
ThíchThích
Với bài này em chỉ cần dùng công thức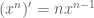 và
và  với
với 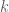 là hằng số.
là hằng số. là tham số, ta có:
là tham số, ta có:


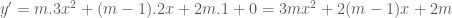
Và xem
ThíchThích
Thay con bai nay thi e phai lam ntn ak.
Chung minh ham so
y=1/(x+1)thoa y^n=((-1)^n.n!)/(x+1)^(n+1)
ThíchThích
Bài này là đạo hàm cấp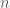 nên em phải chứng minh dùng phương pháp quy nạp.
nên em phải chứng minh dùng phương pháp quy nạp.




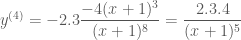




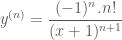 ,
,  .
. bằng phương pháp quy nạp.
bằng phương pháp quy nạp.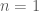 , thay vào
, thay vào  ta được
ta được 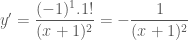
 đúng khi
đúng khi 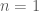 .
. đúng khi
đúng khi  , tức là ta có:
, tức là ta có: 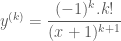 ,
,  .
. đúng khi
đúng khi  .
. ,
,  .
. ta được:
ta được:
 .
. được chứng minh.
được chứng minh. đúng với mọi
đúng với mọi 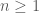 (theo phương pháp quy nạp).
(theo phương pháp quy nạp).
—–
Với
Tập xác định:
Ta viết lại dạng quy nạp các đạo hàm trên như sau:
Từ các công thức trên ta dự đoán
Bước tiếp theo ta chứng minh công thức
– Với
Như vậy
– Giả sử
– Ta sẽ chứng minh
Nghĩa là cần chứng minh
Thật vậy, lấy đạo (cấp 1) hàm hai vế của
Vậy
Suy ra công thức
ThíchThích
thay thu giai cho em bai do dc ko ak
e chua dc hox cach chung mjk
voi ca bai nay` nua~ thay ak
y=xsix thoa xy – 2(y’-sinx)+xy”=0
ThíchThích
– Bước 1:



 vào vế trái của hệ thức cần chứng minh rồi rút gọn để được kết quả bằng
vào vế trái của hệ thức cần chứng minh rồi rút gọn để được kết quả bằng 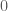 .
.
Tính đạo hàm cấp 1:
– Bước 2:
Tính đạo hàm cấp 2:
– Bước 3:
Thay
ThíchThích
thay e tien the hoi them thay may cau nhung nay gio em hoi thay cung nhieu va thay cung giai giup e nhju uj’nen bay h em cung van hoi nhung thay co the giai bai cua em sau may ban kia cung duoc ak vi ai cung can bai giai cua thay ma nay h thay giai cho e ko ak. e thay cung hoi ngai voi may ban kia` hjhj :). e mong thay se giup do tat ca nhung ai co su dam me ve mon toan hoc :).chuc thay luon co suc khoe tot de theo buoc nhung nguoi hoc sinh nhu bon e ak 🙂
ThíchThích
con bay gio em xin hoi thay them may cau hoi nua
1)Giải hệ phương trình { x+y-can(xy)=1
{can(x^2+3)+can(y^2+3)=4
2)Cho hệ phương trình { x+y=m-2
{x^2+y^2+2x+2y=-m^2+4
a) Tìm để hệ phương trình trên có nghiệm.
b) Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
ThíchThích
b) Tìm giá trị lớn nhất, nhỏ nhất của biểu thức A= xy+2(x+y)+2011 cau b o? tren do thay :D, thay ranh giai jup em ngar thay. tk thay nhju` nkju :))
ThíchThích
Thầy ơi giải giúp em :
Cho a, b, c là ba cạnh của tam giác : 0 <=a <=b<=c. CM (a+b+c)mũ 2 <=9bc
ThíchThích
thay oi giup e bai nek:
viet pt duong tron C biet:a)duong kinh AB voi A(-1,1), B(5,3)
b)tam I(4,-7) VA TIEP XUC VOI 0x
c)di qua 3 diem M(1,-2),N(1,2),P(5,2)
d)di qua A(-1,2),B(-2,3) va tam nam tren duong thang d;3x-y+10=0
ThíchThích
Đây là những dạng bài tập cơ bản.
Em có thể xem thêm tại đây http://toancoban.blogspot.com/search/label/%C4%91%C6%B0%E1%BB%9Dng%20tr%C3%B2n nhé !
ThíchThích
thay ui giup e nha e dang can gap:
tim m de bat phuong trinh sau nghiem dung voi moi gia tri cua x
a)x^2+(m-1)x+1> hoac =0
b)m(m+2)x^2+2mx+2>0
c)mx^2-10x-5<0
ThíchThích
Chú ý: Bất phương trình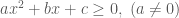 nghiệm đúng với mọi
nghiệm đúng với mọi 
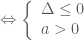
 nghiệm đúng với mọi
nghiệm đúng với mọi 
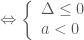
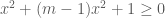 là bất phương trình bậc hai (có hệ số
là bất phương trình bậc hai (có hệ số 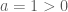 ) nên nó nghiệm đúng với mọi
) nên nó nghiệm đúng với mọi 
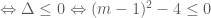

 sau đó chọn khoảng giá trị của
sau đó chọn khoảng giá trị của  để
để  }
}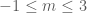 .
. cần tìm là
cần tìm là 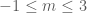 .
. có hệ số
có hệ số 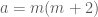 phụ thuộc vào
phụ thuộc vào  nên ta cần xét hai trường hợp.
nên ta cần xét hai trường hợp. .
.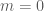 bất phương trình đã cho trở thành
bất phương trình đã cho trở thành 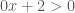 . Bất phương trình này nghiệm đúng với mọi
. Bất phương trình này nghiệm đúng với mọi  .
.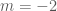 bất phương trình đã cho trở thành
bất phương trình đã cho trở thành  . Bất phương trình này không nghiệm đúng với mọi
. Bất phương trình này không nghiệm đúng với mọi  .
.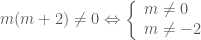 .
.


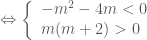
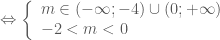

 cần tìm là
cần tìm là 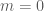 .
.
* Bất phương trình
———————-
Câu a:
Bất phương trình
{Lập bảng xét dấu biểu thức
Giải ta được:
Kết luận: Giá trị của
——-
Câu b:
Nhận xét: Vì bất phương trình
Giải:
* Trường hợp
Với
Với
** Trường hợp
Khi dó bất phương trình đã cho (là bậc hai) nghiệm đúng với mọi
*** Vậy từ hai trường hợp xét trên ta có giá trị của
ThíchThích
Với câu c, em làm tương tự như câu b nhé !
ThíchThích
thay oi! thay viet them nhi thuc niuton di a! cam on thay!
ThíchThích
thay oi giai dum em bai HPT nay dj ak
xy+x+y=x^2-2y^2
xcan(2x)-ycan(x-1)=2x-2y
ThíchThích
Nháp: (*)
(*) , ta có
, ta có
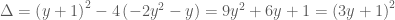
 và
và 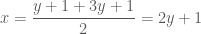 .
. về dạng tích có các thừa số
về dạng tích có các thừa số 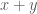 và
và 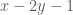 như sau:
như sau:
Với phương trình
Xem đây là phương trình bậc hai với ẩn số
Suy ra phương trình trên có nghiệm:
Từ đây ta có thể biến đổi phương trình
ThíchThích
Lời giải:


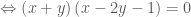
• Trường hợp
Với điều kiện
Trường hợp này hệ đã cho có nghiệm
• Trường hợp
Em tự giải tiếp xem nhé !
ThíchThích
jhuhuhuiuji
ThíchThích
vì sao nghiệm lại = -Y và nghiệm = 2Y + 1
ThíchThích
thay oi gian zum em bai hpt nai nha thay
x^3 + can(x) – 1/x = y^3 + can(y) -1/y
x^2 -2 = can(y+2)
ThíchThích
Nhìn vào phương trình đầu của hệ ta nghỉ đến phương pháp hàm số (vì biểu thức ở hai vế có dạng giống nhau, chỉ khác ẩn). với
với  .
. .
.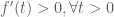 nên hàm số đồng biến trên khoảng
nên hàm số đồng biến trên khoảng  .
. có dạng
có dạng  .
. đồng biến nên từ
đồng biến nên từ  ta có
ta có  .
. .
.
————–
Xét hàm số
Ta có
Nhận thấy
Phương trình
Do hàm số
Thay vào phương trình thứ hai của hệ ta được
Phương trình này em tự giải nhé !
ThíchThích
thầy ơi em đang học bất phương trình nhưng khó hiểu quá. thầy có thể gửi cho em chuyên đề về chứng minh bất pt được không. em cám ơn thầy
ThíchThích
giúp e vs: a;b;c>0
CM: (x2)/a + (y2)/b + (z2)/c >= (x+y+z)2/(a+b+c)
số 2 ở sau là Bình phương
ThíchThích
thay oiu thay co thay chi cho em cach chung minh ham so dong bien va nghich bien tren R dc khong ak.
vi du nhu 2 bai trong SGK nay ak
1) f(x)= x^3 + x -cosx – 4( chung minh ham so dong bien tren R)
2) tim tham so a de ham so dong bien tren R
f(x) 1/3x^3 + ax^2 + 4x + 3
ThíchThích
Em hãy nhớ tính chất (định lý):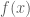 đồng biến trên tập xác định
đồng biến trên tập xác định 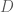 của nó là
của nó là  . Trong đó
. Trong đó 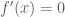 tại hữu hạn điểm thuộc
tại hữu hạn điểm thuộc 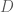 .
.
– Điều kiện đủ để Hàm số
ThíchThích
1. Với hàm số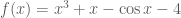 xác định và liên tục trên
xác định và liên tục trên  .
. .
. và
và  với mọi
với mọi  nên
nên 
 ,
,
 .
.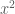 và
và 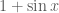 không đồng thời bằng không với mọi
không đồng thời bằng không với mọi  .
. .
. .
.
Ta có
Vì
Mặt khác
Từ đó suy ra
Suy ra
DO dó, hàm số đã cho luôn đồng biến trên
ThíchThích
2. Hàm số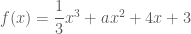 xác định và liên tục trên
xác định và liên tục trên  .
.
 (là tam thức bậc hai).
(là tam thức bậc hai). là
là  .
.
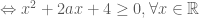 .
.
 .
.
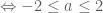 .
.
Điều kiện để hàm số đã cho đồng biên trên
ThíchThích
thay ,trong tam thức vậy hệ số có a âm ta phải đồi chiều dấu à thầy
ThíchThích
thay oi thay con o do khong ak. em muon hoi cai’ nay 1 chuc xiu duoc ko ak
phan luong giac do thay. goc bu` la ntn ak.
tai sao goc sinx = -1 thi => x= -pi/2 + k2pi. vay taj sao goc bu cua no lai la 3pi/2 ak
ThíchThích
thay oi thay giai zum em bai nay dc hok ak
Rut gon Bieu thu: A=(3+4can3)/can6+can2-can5
ThíchThích
Bài toán này thuộc chương trình lớp 9 phải không em ?
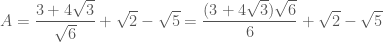
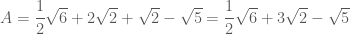
======
EM chỉ cần trục căn thức ở mẫu rồi rút gọn bình thường.
ThíchThích
Thầy giải giúp em bai này với:
CMR: cos3a + cos3b + cos3c = 1 – 4sin1,5asin1,5bsin1,5c
ThíchThích
EM xem lại đề coi có điều kiện gì của không nhé !
không nhé !
ThíchThích
Dạ thưa thầy em quên không ghi thêm a,b, c là các góc trong 1 tam giác
ThíchThích
thay oi thay nham` de` uj` thay uj de` bai cua? no ne`
A=3+4can3/(can6+can2-can5) day moi la de` cua no do thay`
ThíchThích
thay chi lai cho e cai goc’ bu` cua luong giac duoc khong thay. em bi mat can ban cai do’ uj`.mong thay giup do em. em cam on thay 🙂
ThíchThích
thay giai ho em bai nay nhe! trog ko gian oxyz cho hinh vuong ABCD co m la trug diem cua bc, ptdt DM:x-y-2=0 va c(3,-3). biet dinh A thuoc dt:3x+y-2=0.XDtoa do cua A,B,D
ThíchThích
thay oi cho them nhieu de moi dj chu de cua thay em lam het roi
ThíchThích
thay giai dum e bai toán này với
tìm số hạng không chứa X trong khai triển nhị thức Newton của [2X+1/(căn bậc năm của X)]^18
ThíchThích
sao thâỳ ko giải bài ni jum e với , e ko biết cách làm nơi , khó quá thầy ạ
ThíchThích
Rồi.
Thầy đã trả lời ở cầu hỏi của em. Em xem lại nhé (tại đây)!
ThíchThích
Ta có:
Điều kiện là
Do đó ta cần xét hai trường hợp:
Trường hợp
Suy ra:
Mỗi Số hạng của khai triển có dạng
Số hạng không chứa
Trường hợp này ta có số hạng cần tìm là:
==
Trường hợp
Khi đó
Số hạng không chứa
Vậy trường hợp này số hạng không chứa
====
Tóm lại: Số hạng cần tìm bằng
ThíchThích
Cách khác là khai triển nhị thức đã cho thành tổng của 19 số hạng. .
.![\sqrt[n]{{{a^m}}} = {a^{\frac{m}{n}}}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7B%7B%7Ba%5Em%7D%7D%7D+%3D+%7Ba%5E%7B%5Cfrac%7Bm%7D%7Bn%7D%7D%7D+&bg=ffffff&fg=4e4e4e&s=0&c=20201002) với điều kiện
với điều kiện  .
. và
và  để biến đổi căn thành lũy thừa.
để biến đổi căn thành lũy thừa.
Sau đó rút gọn và chỉ ra số hạng không chứa
====================
Chú ý rằng: Ta chỉ viết được
Do vậy, ở bài giải trên thầy phải xét các trường hợp
ThíchThích
thầy ơi , 2 tH kết quả giống nhau , là vì sao thầy
ThíchThích
Vì khi khai triển biểu thức ta chỉ thu được một kết quả.
Ta xét 2 trường hợp là để biến đổi căn thành lũy thừa để dễ rút gọn và không biến đổi sai thôi.
ThíchThích
thầy ơi giúp em bai này với .hix
viết phuơng trình các cạch của tam giác ABC biết B(2,7) ,đuờng cao qua A có phuơng trình là: 3x+y+11=0 , trung tuyen qua C có phuơng trình là x+2y+7=0
Em cảm ơn thầy rất nhiều.
ThíchThích
Đường thẳng BC đi qua B và vuông góc với đường cao qua A : nên có phương trình
nên có phương trình

 do đó tọa độ của C là nghiệm của hệ:
do đó tọa độ của C là nghiệm của hệ:

 .
.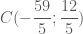 .
.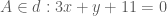 là
là 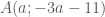 .
.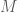 của đoạn
của đoạn  có tọa độ
có tọa độ  .
.
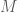 thuộc đường trung tuyến qua
thuộc đường trung tuyến qua  có phương trình
có phương trình  nên ta có
nên ta có
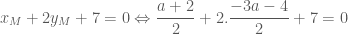
 .
.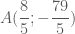 .
.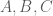 em tự viết phương trình các đường thẳng chứa các cạnh AB, AC nhé !
em tự viết phương trình các đường thẳng chứa các cạnh AB, AC nhé !
ĐIểm C thuộc đường thẳng BC và đường trung tuyến có phương trình
Hệ này có nghiệm
Suy ra
Gọi tạo độ của
Trung điểm
Suy ra
========
Có tọa độ của
ThíchThích
thay oi thay co viec gi ban ha ma em khong thay thay` tra loi cau hoi cua em :((
ThíchThích
thay oi thay nham` de` uj`. thay uj de` bai cua? no ne`
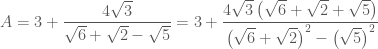
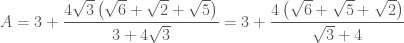


A=3+4can3/(can6+can2-can5) day moi la de` cua no do thay`
========================
Lần sau em nhớ gõ bằng Tiếng Việt, có dấu đầy đủ nhé !
————-
Đến đây em quy đồng, rút gọn là xong !
ThíchThích
thầy ơi giúp em bai này với ah.
B1:viết phưong trình các cạnh của tam giác ABC.Biết A(2;-4) và 2 đường phân giác tong có phương trình là : x+y-2=0 và x-3y-6=0.
B2:cho tam giác ABC cân tại A có phuơng trình cạnh AB : x-y+5=0 cạnh BC : x+2y=0 .viết phương trình cạnh AC biết rằng AC đi qua M(4,2)
ThíchThích
Bài 1: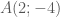 không thuộc hai đường thẳng
không thuộc hai đường thẳng  và
và  .
.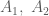 lần lượt là điểm đối xứng của
lần lượt là điểm đối xứng của 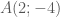 qua các đường thẳng
qua các đường thẳng  .
.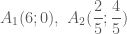 . {Em tự làm việc này nhé !}
. {Em tự làm việc này nhé !}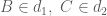 .
.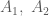 thuộc đường thẳng chứa cạnh
thuộc đường thẳng chứa cạnh  (do tính đối xứng trục của các đường phân giác ).
(do tính đối xứng trục của các đường phân giác ). đi qua
đi qua 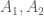 có phương trình
có phương trình 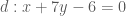 . {Em tự làm việc này nhé !}
. {Em tự làm việc này nhé !}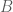 thuộc
thuộc  nên tọa độ của
nên tọa độ của 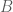 là nghiệm của hệ
là nghiệm của hệ

 .
.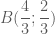 .
. nên ta tìm được
nên ta tìm được 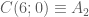 .
.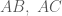 nhé !
nhé !

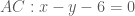 .
. là đường thẳng qua
là đường thẳng qua  và
và  .
. .
. . Tọa độ của
. Tọa độ của 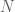 là nghiệm của hệ
là nghiệm của hệ
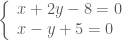
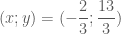 .
. .
.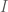 là trung điểm của đoạn
là trung điểm của đoạn 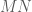 , ta có
, ta có  .
. là đường thẳng đi qua
là đường thẳng đi qua 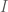 và vuông góc với
và vuông góc với  .
.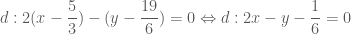
 cân tại
cân tại  và cạnh
và cạnh  đi qua
đi qua 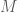 nên cạnh
nên cạnh  đi qua
đi qua 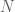 .
. là đường thẳng
là đường thẳng  đi qua
đi qua 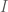 và vuông góc với
và vuông góc với  và
và 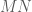 .
.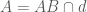 là nghiệm của hệ
là nghiệm của hệ

 .
. .
. cần tìm đi qua
cần tìm đi qua  nên có phương trình
nên có phương trình  .
.
====
Nhận thấy điểm
Gọi
Ta tìm được
Giả sử
Ta có
Đường thẳng chứa
Ta nhận thấy,
Hệ này có nghiệm
Suy ra
Tương tự, điểm
Từ đó em tự viết phương trình các đường thẳng chứa cạnh
Đáp số:
=====================
Bài 2:
==
Gọi
Phương trình của
Gọi
Hệ này có nghiệm
Suy ra
Gọi
Gọi
Ta có phương trình
Vì tam giác
DO đó đường cao hạ từ đỉnh
Suy ra tọa độ của
Hệ này có nghiệm
Suy ra
ĐƯờng thẳng
ThíchThích
Bài 2 Có thể làm theo nhiều cách khác. Em tự tìm xem nhé !
ThíchThích
e cám ơn thầy ,
ThíchThích
phuơng trình cạnh BC có phuơng trình la:x+2y=0.ấy thầy.
em cảm ơn thầy nhiều .
ThíchThích
thầy giải dúp e bài ni với , e cám ơn thầy nhìu
1,Trong kg Oxyz cho 3 điểm A(2;0;1) B(1;0;0) C(1;1;1) và mp (P): x+y+z-2=0 , viết phương trình mặt cầu đi qua 3 điểm A,B,C và có tâm thuộc mp(P)
2, trong mp tọa độ Oxy , cho điểm M di động trên elip (E): 9x^2 +16y^2 =144, H và K là hình chiếu vuông góc của M lên hai trục tọa độ . Tìm M để diện tích tứ giác OHMK lớn nhất .
ThíchThích
Gọi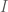 là tâm mặt cầu cần tìm, ta có
là tâm mặt cầu cần tìm, ta có  .
. thuộc mặt phẳng trung trực của các đoạn
thuộc mặt phẳng trung trực của các đoạn  .
. đi qua trung điểm
đi qua trung điểm  và vuông góc với
và vuông góc với  nên nhận
nên nhận  làm vecto pháp tuyến, do đó có phương trình:
làm vecto pháp tuyến, do đó có phương trình:

 là:
là:

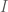 thuộc các mặt phẳng
thuộc các mặt phẳng 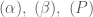 nên có tọa độ là nghiệm của hệ
nên có tọa độ là nghiệm của hệ

 . Suy ra
. Suy ra  .
. .
. .
.
Do đó
* Mặt phẳng trung trực của đoạn
* Tương tự, ta có phương trình mặt phẳng trung trực của đoạn
* Tâm
Hệ này có nghiệm
Bán kính mặt cầu:
Vậy phương trình mặt cầu cần tìm là:
ThíchThích
Bài 2: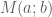 . Vì
. Vì  nên ta có
nên ta có  .
. lần lượt là hình chiếu của
lần lượt là hình chiếu của 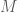 trên trục hoành và trục tung, ta có
trên trục hoành và trục tung, ta có 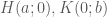 .
. bằng
bằng 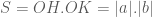 .
.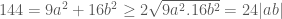 .
.
 .
.
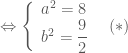 .
. có bốn nghiệm:
có bốn nghiệm:
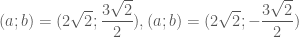 ,
,
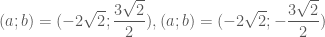 .
.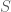 đạt giá trị lớn nhất bằng
đạt giá trị lớn nhất bằng 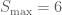 .
.
 .
.
====
Gọi tọa độ của
Gọi
Diện tích hình chữ nhật
Áp dụng bất đẳng thức Cô-si ta có
Dấu = xảy ra khi và chỉ khi
Hệ
Từ đó suy ra diện tích
Vậy có bốn điểm thỏa yêu cầu bài toán là:
ThíchThích
đề toán Tn năm nay dể quá thầy nhỉ
ThíchThích
thầy ơi.em lam bai 1 rồi nhưng mà làm sao kết qua k có đúng.Thầy làm lại giúp em đuợc không ah.Em cảm ơn thầy nhiều.
ThíchThích
Thầy đã làm cả 2 bài rồi em à. Em xem lại nhé !
ThíchThích
Thầy giải giúp e mấy câu này với:
1 . tìm m để pt l x^4-5x^2+4 l = log(m) có 6 ngiệm
2. gpt :sin2x + sinx – 1/(2sinx)-1/(sin2x)=2cotg2x
3.tìm m để pt có nghiệm x thuộc [0;1+ căn(3)] .
pt :m[căn(x^2-2x+2)+1]+x(2-x) = căn(xy)+ 3.căn(yz) + 5.căn(zx) .
5. giải hpt:(!) :x+ căn(x^2-2x+2)=3^(y-1)+1 . (!!) :y+căn(y^2-2y+2)=3^(x-1)+1 (x,y thuộc R)
ThíchThích
thầy ơi cái mặt người là chữ X , thầy giải xog pm sớm lại cho e với , e cám ơn thầy !
ThíchThích
thay oi e co bai toan nay mun hoi thay .cho d1: x-7y+17 =0,d2:x+y-5=0 viet ptrinh d di wa M(0,1) va tao voi d1,d2 tai giao diem hai duong thang d1,d2
ThíchThích
thầy ơi, em có bài toán này muốn hỏi thầy: giải hệ phương trình vô tỉ; x căn (1-y2)=1/4 và y căn (1-x2)=1/4 thì làm thế nào ạ?

ThíchThích
Điều kiện: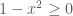 và
và  .
.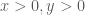 .
.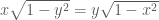
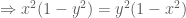

 thay vào hệ đã cho ta có:
thay vào hệ đã cho ta có: 
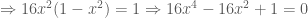

 thỏa mãn điều kiện.
thỏa mãn điều kiện. .
. không thỏa mãn hệ đã cho.
không thỏa mãn hệ đã cho.
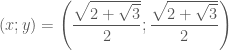
 : EM tự giải nhé !
: EM tự giải nhé !
Mặt khác, do vế phải của hai phương trình là số dương nên ta phải có:
Từ hệ ta có
Trường hợp
Giải ta được:
Giá trị
Suy ra
Giá trị
Trường hợp này hệ có một nghiệm:
Trường hợp
ThíchThích
Thầy ơi, thầy giúp em bài này với: Trong mặt phẳng hệ tọa độ Oxy, xác định tọa độ đỉnh C của tam giác ABC biết rằng hình chiếu vuông góc của C trên AB là điểm H(-1,-1) đường phân giác trong góc A có phương trình 😡 – y + 2 = 0 và đường cao kẻ từ B có phương trình: 4x+ 3y- 1= 0
ThíchThích
Vì nên gọi tọa độ của
nên gọi tọa độ của 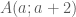 .
.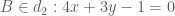 nên gọi tọa độ của
nên gọi tọa độ của 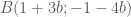 .
. là hình chiếu vuông góc của
là hình chiếu vuông góc của  trên đường phân giác trong góc
trên đường phân giác trong góc  trên
trên  .
.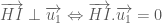 .
. là vectơ chỉ phương của
là vectơ chỉ phương của  ).
).
 .
. .
.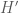 là điểm đối xứng của
là điểm đối xứng của  qua đường thẳng
qua đường thẳng  . Khi đó,
. Khi đó,  là trung điểm của
là trung điểm của 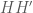 .
. .
. chứa cạnh
chứa cạnh  .
.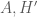 đối xứng với đường thẳng
đối xứng với đường thẳng  qua
qua  nên chứa cạnh
nên chứa cạnh  .
.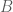 có phương trình
có phương trình 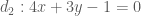 . Đường cao này vuông góc với đường thẳng
. Đường cao này vuông góc với đường thẳng  .
.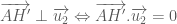 .
.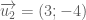 là vectơ chỉ phương của
là vectơ chỉ phương của 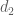 ).
).
 .
. .
.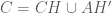 .
. đi qua
đi qua  và vuông góc với
và vuông góc với  , phương trình
, phương trình  .
.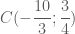 .
.
Vì
Gọi
Ta có
(Với
Suy ra
Họi
Từ đó ta có
Đường thẳng đi qua
Đường thẳng đi qua
Mà đường cao đi qua
Từ đó suy ra
(Với
Suy ra
Lúc này
=====
Em tự viết phương trình
Rồi suy ra tọa độ của
ThíchThích
thầy ơi, thầy giải giúp em bai toán đấy với. Mà cái mặt người đấy là chữ x đấy ạ. Em cảm ơn thầy ạ
ThíchThích
Tại sao thầy không hướng dẫn bài cho e?
ThíchThích
Bận ăn Tết nên thầy không lên mạng em à. Em thông cảm nhé !
====
Em xem lời giải tại đây.
ThíchThích
Em cảm ơn thầy nhiều ạ 🙂
ThíchThích
Thầy giúp con bài này với: 1. Trong mặt phẳng hệ tọa độ Oxy, cho hình chữ nhật ABCD có I(6;2) là giao điểm hai đường chéo AC, BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm E của cạnh CD thuộc đt đenta: x-y+5=0. Viết phương trình đt AB.
2. Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có M(2;0) là trung điểm cạnh BC. Đường trung tuyến và đường cao qua đỉnh A lần lượt có pt là: 7x-2y-3=0 và 6x-y-4=0. Viết phương trình đường thẳng AC.
3. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh A(3;-7), trực tâm H(3;-1), tâm đường tròn ngoại tiếp I(-2;0). Xác định tọa độ đỉnh C và biết C có hoành độ dương.
ThíchThích
Bài 1: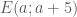 là trung điểm của
là trung điểm của  .
. là trung điểm của cạnh
là trung điểm của cạnh  . Khi đó
. Khi đó 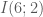 là trung điểm của
là trung điểm của  .
. .
.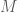 thuộc đường thẳng
thuộc đường thẳng  nên
nên  .
.

Giả sử
Gọi
Suy ra tọa độ của
Vì
Phương trình này vô nghiệm nên bài toán không có nghiệm hình.
ThíchThích
Bài 2:
Trung tuyến đi qua đỉnh
===
Kiểm tra lại ta thấy
ThíchThích
Bài 3: .
. là trọng tâm tam giác
là trọng tâm tam giác  .
. .
. .
.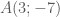 và
và  suy ra tọa độ trung điểm
suy ra tọa độ trung điểm 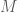 của cạnh
của cạnh  là
là 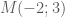 .
. đi qua điểm
đi qua điểm 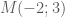 và vuông góc với
và vuông góc với  có phương trình:
có phương trình:  .
.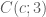 với
với 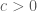 .
.
 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác  nên
nên 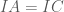 .
.

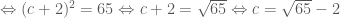 .
. .
.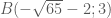 .
.
Hãy chứng minh:
Gọi
Từ hệ thức trên suy ra:
Suy ra tọa độ điểm
Từ điểm
Đường thẳng chứa cạnh
Nên tọa độ của
Vậy
====
Lập luận tương tự tìm được
ThíchThích
Thầy ơi, nếu bài 3 con chứng minh H là trung điểm của A’H thì phải làm thế nào ạ? Con cảm ơn thầy nhiều!
ThíchThích
Con đánh nhầm thầy ạ. CM: M là trung điểm của A’H mà không phải chứng minh BHCA’ là hbh
ThíchThích
Bài 1, hình như thầy làm nhầm rồi thầy ơi
ThíchThích
cho tam giác abc có a(2:7) và phương trình trung tuyến và đường cao kẻ từ 2 đỉnh khác nhau là 3x+y+11=0 và x+2y+7=0. viết pt các cạnh còn lại.giải giúp em thầy ơi.
ThíchThích
thầy ơi giúp em làm bài này với :3x mũ 2 – 7x cộng 2 . thầy cho em công thức cụ thể nha thầy . em có công thức nhưng em không hiểu . thầy nhơ giải theo toán lớp 7 và thật cụ thể nha thầy . cám ơn thày .
ThíchThích
Thầy cho em hỏi nếu viết phương trình chính tắc của đường tròn mà không ghi chính tắc thì có sai không ạ!
ThíchThích
nick docaolong cua thay là nick gì đấy ạ
ThíchThích
thầy ơi chỉ giúp em mấy trang có nhiều bài tập giải pt, hệ pt bằng cách sử dụng tính đơn điệu của hàm số có lời giải với ạ
ThíchThích
thầy cho em hỏi muốn xem đề đại học thì vào phần nào
ThíchThích