Đề thi thử đại học số 8 năm 2012- (Tạp chí Toán học tuổi trẻ)
ĐỀ THI THỬ SỐ 08
LỜI GIẢI CHI TIẾT MỖI Ý ĐƯỢC ĐĂNG TRÊN MỘT TRANG RIÊNG.
HÃY CLICK VÀO TỪNG SỐ TRANG CUỐI BÀI VIẾT NÀY ĐỂ XEM.
Câu I: Cho hàm số có đồ thị
.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Viết phương trình tiếp tuyến với biết tiếp tuyến tạo với hai đường tiệm cận của
thành một tam giác có bán kính đường tròn nội tiếp lớn nhất.
Câu II:
1. Giải phương trình .
2. Giải bất phương trình .
Câu III: Tính diện tích hình phẳng giới hạn bởi các đường và các đồ thị hàm số
,
.
Câu IV: Cho hình lăng trụ đứng , đáy ABC là tam giác vuông có
, góc giữa đường thẳng
và mặt phẳng
bằng
. Gọi M là trung điểm cạnh
. Tính khoảng cách từ điểm M đến mặt phẳng
.
Câu V. Tìm các số thực thỏa mãn hệ phương trình
Câu VIa:
1. Trong mặt phẳng tọa độ , cho các điểm
. Tìm tọa độ điểm M sao cho góc
và khoảng cách từ M đến đường thẳng AB bằng
.
2. Trong không gian với hệ tọa độ , cho
. Lập phương trình mặt phẳng qua OA, cắt đoạn BC tại D sao cho tỉ số thể tích của các khối tứ diện OABD và OACD bằng 3.
Câu VIIa:
Tìm tất cả các số phức z thỏa mãn phương trình .
Câu VIb:
1. Trong mặt phẳng tọa độ , cho điểm
là một trong hai giao điểm của đường tròn
và đường tròn
. Viết phương trình đường thẳng đi qua A cắt
theo hai dây cung khác nhau có độ dài bằng nhau.
2. Trong không gian với hệ tọa độ , cho hình lập phương
có A trùng gốc tọa độ, các điểm
. Viết phương trình mặt phẳng (P) qua
, biết (P) tạo với BC và
những góc bằng nhau.
VIIb:
Xét khai triển thành đa thức
.
Tìm hệ số .
Posted on 21/05/2012, in ôn thi đại học, Toán lớp 12 and tagged đề thi thử đại học năm 2012. Bookmark the permalink. 55 bình luận.

thưa thầy ! bài này em không chọn x= m+1 mà em tìm tạo độ A,B theo pt tiếp tuyến với 2 điểm tiệm cận đc không thầy, , A (1 ;(2x-4)/(x-1)) . B( 2x-1; 2) rồi tìm IA,IB như thầy, không biết đúng không , mà kết quả vẫn giống như thầy
ThíchThích
Được chứ em.
ThíchThích
em cảm ơn thầy nhiều lắm
ThíchThích
thầy ơi ! bài giải pt hàm số Mũ mình đặt u,v đc không thầy, nếu đc em thấy dể hơn thầy ah.
em cảm ơn thầy nhiều
ThíchThích
ĐƯợc chứ em. CÓ nhiều cách giải bài toán này mà.
Thầy chọn cách biến đổi về dạng tích để trình bày.
ThíchThích
cảm ơn thầy nha!
ThíchThích
thầy ơi, bài tính diện tích có dấu trị tuyệt đối, mà thầy em dạy là không đc đưa ra ngoài mà thầy, thày em nói là dù biết + hay _ cũng không đc đưa ra
ThíchThích
Kiến thức này được SGK cung cấp và chấp nhận cách làm đó.
Nếu em không thích thì xét dấu để khử dấu gttđ .
ThíchThích
Thầy xem lại kết luận câu II2 nhé
ThíchThích
thầy ơi câu II.1 sao đặt nhân tử chung là 8sin^(2){2x} được
ThíchThích
Thầy đánh nhầm đề.
Thầy đã sửa lại đề rồi.
ThíchThích
bai nay giong de thi cao dang nam ngoai
ThíchThích
sao khong co dieu kien de can ton tai vay thay
ThíchThích
Điều kiện đó thầy đã lồng ghép trong lúc lấy nghiệm em à.
ThíchThích
em mog thay cho ra them de vi em da lam het cac de thay cho ra roi
ThíchThích
da thua thay sao khong goi duong thang di qua A co vtpt n(a,b) lam vay nhanh hon thay a
ThíchThích
em thua thay sao lai co mat phang quaAA1 chua truc oz la ax+by=0
ThíchThích
Mặt phẳng chứa trục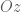 có dạng phương trình là
có dạng phương trình là 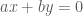 mà em.
mà em.
Em xem lại kiến thức ở Sách giáo khoa Hình học 12 nhé !
ThíchThích
em thua thay sao lai co ptmp qua AA1 chua truc oz la ax+by=o
ThíchThích
thay giai giup em bai nay duoc khong thay
trong mat phang oxy cho hinh vuong ABCD biet c(3:2) phuong trinh duong thang DM :4x-3y-1=0 voI M la trung diem cua doan BC va dinh A thuoc duong thang d:x+y-3=0 tim toa do cac dinh A ,B,D
ThíchThích
Gọi tọa độ điểm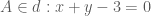 là
là  .
.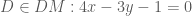 là
là  .
.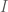 của đoạn
của đoạn  là:
là: 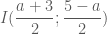 .
.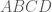 là hình vuông đó là
là hình vuông đó là 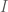 là trung điểm của đoạn
là trung điểm của đoạn 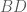 .
. .
.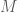 của cạnh
của cạnh  là:
là:  .
. nên ta có
nên ta có 
 .
. và
và 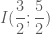 .
.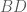 qua
qua 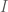 và vuông góc với
và vuông góc với  nên nhận
nên nhận 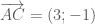 làm vecto pháp tuyến do đó có phương trình:
làm vecto pháp tuyến do đó có phương trình:
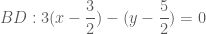
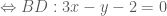 .
.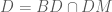 nên tọa độ của
nên tọa độ của 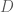 là nghiệm của hệ
là nghiệm của hệ

 .
. .
. .
.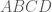 là hình thoi (hình bình hành có hai đường chéo vuông góc).
là hình thoi (hình bình hành có hai đường chéo vuông góc).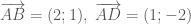 nên
nên 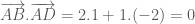 .
.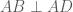 .
.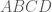 là hình vuông với
là hình vuông với  .
.
Gọi tọa độ điểm
Tọa độ trung điểm
Điều kiện cần để
Từ đó suy ra
Suy ra tọa độ trung điểm
Vì
Suy ra
Đường thẳng
Điểm
Hệ này có nghiệm
Suy ra
Từ đó suy ra
Nhận xét với các điều kiện nêu trên thì tứ giác
Ta có
Suy ra
Vậy tứ giác
ThíchThích
Hay lam thay oi……..^^!!
em cam” on thay nhieu
ThíchThích
thầy ơi!!, câu VI.a.1/ góc giữa MA,AB nếu kéo dài AB ra thì đó là góc 45 độ thì sao thầy, vậy cos nó bàng căn 2/2 thì sao thầy..em cảm ơn thay.
ThíchThích
Em cần chú ý: Góc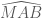 có đỉnh
có đỉnh  nên bằng góc giữa hai vecto
nên bằng góc giữa hai vecto  và
và 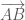 .
.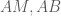 .
.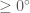 và không vượt quá
và không vượt quá  .
.
Chứ không phải bằng góc giữa hai đường thẳng
Góc giữa hai đường thẳng luôn có số đo
ThíchThích
em cam on thay nhieu:
thay giai gium em bai nay duoc khong thay
cho ba so thuc duong x,y,z thoa x+y+z<=1/4 tim gia tri nho nhat cua A
A=x+y+z+1/x+2y+3z+1/3x+y+2z+1/2x+3y+z
ThíchThích
Thầy có hướng giải như sau, em tham khảo nhé !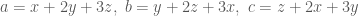 .
.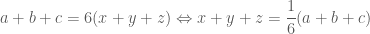 .
.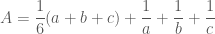 . (*1*)
. (*1*) là các số dương thì
là các số dương thì 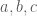 cũng là các số dương.
cũng là các số dương.
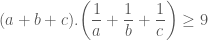
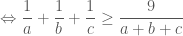 . (*2*)
. (*2*)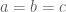 .
. . ta có
. ta có  .
. .
.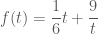 với
với 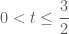 , ta có:
, ta có:
![f'(t)=\dfrac{1}{6}-\dfrac{9}{t^2}=\dfrac{t^2-54}{6t^2} < 0, \forall t \in \left( 0; \dfrac{3}{2} \right]](https://s0.wp.com/latex.php?latex=f%27%28t%29%3D%5Cdfrac%7B1%7D%7B6%7D-%5Cdfrac%7B9%7D%7Bt%5E2%7D%3D%5Cdfrac%7Bt%5E2-54%7D%7B6t%5E2%7D+%3C+0%2C+%5Cforall+t+%5Cin+%5Cleft%28+0%3B+%5Cdfrac%7B3%7D%7B2%7D+%5Cright%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
. giảm trên nữa khoảng
giảm trên nữa khoảng ![\left( 0; \dfrac{3}{2} \right]](https://s0.wp.com/latex.php?latex=%5Cleft%28+0%3B+%5Cdfrac%7B3%7D%7B2%7D+%5Cright%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
. .
. bằng
bằng  đạt được khi
đạt được khi 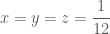 .
.
=============
Đặt
Ta có
Khi đó
Với
VÀ ta luôn có
Dấu = xảy ra khi và chỉ khi
Đặt
Từ (*1*) và (*2*) , ta có
Xét hàm số
Suy ra hàm số
Do đó
Vậy giá trị nhỏ nhất của
ThíchThích
Thầy ơi! em có bài pt em giải không ra, thầy giair giúp em dược không thầy
5 căn của (x+1)^3=21 căn (x+1)+căn[(x^2-x-20)*(5x+9)]+5 căn(x^2-x-20)
em cảm ơn thầy nhiều
ThíchThích
Thầy có hướng giải sau, em tham khảo nhé !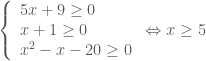


![\Leftrightarrow \sqrt{x+1} \left[5(x+1)-21 \right]=\sqrt{x^2-x-20} \left(\sqrt{5x+9}+5 \right) \;\; (2)](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%5Csqrt%7Bx%2B1%7D+%5Cleft%5B5%28x%2B1%29-21+%5Cright%5D%3D%5Csqrt%7Bx%5E2-x-20%7D+%5Cleft%28%5Csqrt%7B5x%2B9%7D%2B5+%5Cright%29+%5C%3B%5C%3B+%282%29&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
. .
.

 . (vì
. (vì  )
)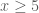 thì hai vế của
thì hai vế của  đều không âm.
đều không âm.

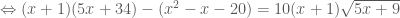

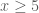 thì hai vế của
thì hai vế của 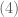 đều không âm.
đều không âm.
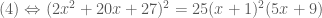

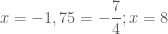 nên ta biến đổi phương trình cuối này về dạng tích}
nên ta biến đổi phương trình cuối này về dạng tích}

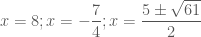 .
. thỏa điều kiện của phương trình đã cho.
thỏa điều kiện của phương trình đã cho.

================
ĐIều kiện:
Với điều kiện trên ta có:
Lại có
DO đó
Với điều kiện
Bình phương hai vế ta được phương trình tương đương.
Với điều kiện
Bình phương hai vế ta được phương trình tương đương.
{Dùng máy tính cầm tay dò tìm nghiệm ta được nghiệm
Phương trình này có bốn nghiệm:
Chỉ có hai nghiệm
===
Kết luận: Phương trình đã cho có hai nghiệm
ThíchThích
Dạ, em cảm ơn thầy. Tại em đoán nghiệm từ đầu là x=8 rồi đưa về pt tích, giải ra được x=8 còn trong ngoặc không biết làm luôn. em cảm ơn thầy nhiều.
ThíchThích
em cam on thay nhieu mlong thay giup do em nhieu
ThíchThích
thầy ơi,em đọc bài thầy giải rất hay…Em có bài này nhờ thầy giúp ạ:4sinx + cosx = cos2x + 3
ThíchThích
thầy ơi! câu 1 ,em làm bằng cách nhận xét ,để Rmax thì AI=BI cũng ra kết quả giống thầy nhưng có vẻ ko đúng ,vậy để làm theo cách này em cần trình bày như thế nào ạ? cảm ơn thầy nhiều ạ.
ThíchThích
thầy ơi, sao các đề số 3, 5 của toán học va tuổi trẻ thầy hok giải.
ThíchThích
thay oi! giup em bai nay voi. tich phan tu 0 den pi/4 cua sin4x/((cosx)^2.can((tan4x)^4 +1))
ThíchThích
Có phải em hỏi bài này không ?

ThíchThích
da phai thay!thay giai giup em voi, em cam on thay.
ThíchThích
Cảm ơn thầy rất nhiều!
ThíchThích
thay oi, em co bai toan nay em giai khong ra, thay giup em nha. em dang can gap. cam on thay nhieu.
Cho ham so: y=x^3+(1-2m)x^2+(2-m)x+m+2
tìm m để đồ thị có tiếp tuyến tạo với dt d: x+y+7=0 goc a, biết cosa=1/căn 26..em tìm được hsg k rồi nhưng không trong pt có 2 ẩn xo và m, làm sao tìm ra m vậy thầy. em cảm ơn thầy nhiều..
ThíchThích
Gọi là hệ số góc của tiếp tuyến thỏa yêu cầu bài toán.
là hệ số góc của tiếp tuyến thỏa yêu cầu bài toán.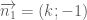 .
. là
là  .
.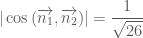
 .
.



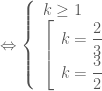


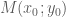 là tiếp điểm của tiếp tuyến nói trên và đồ thị.
là tiếp điểm của tiếp tuyến nói trên và đồ thị. có nghiệm {ẩn
có nghiệm {ẩn  }.
}.
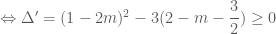

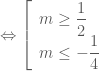 .
. cần tìm để yêu cầu bài toán được thỏa mãn là
cần tìm để yêu cầu bài toán được thỏa mãn là  hoặc
hoặc  .
.
Ta có một vecto pháp tuyến của tiếp tuyến là
Vecto pháp tuyến của đường thẳng
Theo giả thiết, ta có
===
Ta có
Giả sử
Khi đó phương trình
Vậy giá trị của
ThíchThích
thầy ơi, chỉ xét y’=0 có nghiêm thôi hả thầy..dạ, em cảm ơn thầy
ThíchThích
thay oi thay co the lam ho em bai nay dk hok ak .tinh tich phan tu 0 den pi/2 cua(dx / (2+sin2x) ) .thanks thay nhju
ThíchThích
thay giai giup em bai nay duoc k thay
trong mat phang oxy cho tam giac ABC can co (AB=AC) biet pt canh AB, AC lan luot la d1:2x+y-1=0 ,d2:x+4y+3=0 viet pt duong cao qua dinh B cua tam giac ABC
ThíchThích
thay oj thay thế b=3 vao M saj roj, dang le faj la M(-2;1)
ThíchThích
thua thay.thay co the giai giup em bai toan ny dc k:”trong mp he toa do OXY,cho tam giac ABC biet A(5;2).Pt duong trung truc canh BC,duong trung tuyen CM lan luot l x+y-6=0,2x-y
+3=0.Tim toa do cac dinh cua tg ABC.em cam on thay.
ThíchThích
Gọi tọa độ điểm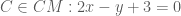 là
là  .
. nên nhận
nên nhận 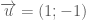 làm vecto pháp tuyến.
làm vecto pháp tuyến.
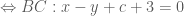 .
. là trung điểm của cạnh BC. Khi đó
là trung điểm của cạnh BC. Khi đó  nên tọa độ của
nên tọa độ của 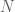 là nghiệm của hệ:
là nghiệm của hệ:

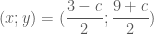 .
. .
.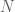 là trung điểm của cạnh
là trung điểm của cạnh  nên ta suy ra tọa độ của đỉnh
nên ta suy ra tọa độ của đỉnh 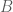 là:
là:
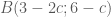 .
.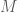 là trung điểm của cạnh
là trung điểm của cạnh  ta có tọa độ của
ta có tọa độ của 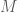 là:
là:
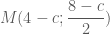 .
.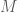 thuộc đường trung tuyến
thuộc đường trung tuyến  nên ta có phương trình:
nên ta có phương trình:
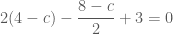
 .
. là:
là:
 .
.
ĐƯờng thẳng BC đi qua C và vuông góc với đường trung trực
Phương trình đường thẳng BC là
Gọi
Giải hệ ta được
Suy ra
Vì
Gọi
Do
Từ đó ta có tọa độ các đỉnh
ThíchThích
thầy ơi giúp em bài này, em giải ra x=2 nhưng thử lại không đúng (em đặt ĐK rồi rút mũ ra ngoài để đơn giản) : (3/2).log(1/4)(x+2)^2 – 3 = log(1/4)(4-x)^3 + log(1/4)(x+6)^3 gần thi rồi, thầy ráng giúp tụi em nhe thầy, em cám ơn!
ThíchThích
Với phương trình: .
.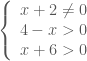 .
.

 .
. .
. .
.
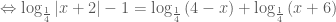
![\Leftrightarrow {\log _{\frac{1}{4}}}\left( {4\left| {x + 2} \right|} \right) = {\log _{\frac{1}{4}}}\left[ {\left( {4 - x} \right).\left( {x + 6} \right)} \right]](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%7B%5Clog+_%7B%5Cfrac%7B1%7D%7B4%7D%7D%7D%5Cleft%28+%7B4%5Cleft%7C+%7Bx+%2B+2%7D+%5Cright%7C%7D+%5Cright%29+%3D+%7B%5Clog+_%7B%5Cfrac%7B1%7D%7B4%7D%7D%7D%5Cleft%5B+%7B%5Cleft%28+%7B4+-+x%7D+%5Cright%29.%5Cleft%28+%7Bx+%2B+6%7D+%5Cright%29%7D+%5Cright%5D&bg=ffffff&fg=4e4e4e&s=0&c=20201002) .
.

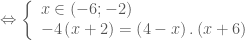 hoặc
hoặc 
 hoặc
hoặc 
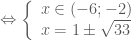 hoặc
hoặc 
 hoặc
hoặc 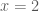 .
. .
.
Ta có điều kiện:
Chú ý:
Ta có
Vậy phương trình đã cho có hai nghiệm
ThíchThích
thay giai giup em bai nay dc k thay
trong mat phang oxy cho tam giac ABC co dien tich bang 2 co phuong trinh canh AB la x-y=0 co diem I(2;1) trung diem canh BC tim toa do diem M trung diem canh AC
ThíchThích
Thay oi! e co bai nay giai hoai cung khong ra. Thay giai gium em duoc khong thay ?
cho y= x^3 + 3x^2 + mx + 1 (C) , y=1 (d). Tim m de (d) cat (C) tai 3 diem A, B, C trong do A la diem co dinh sao cho tiep tuyen tai B cat tiep tuyen tai C tai D va dien tich tam giac BCD lon nhat.
Em cam on thay !!!
ThíchThích
Xét hàm số đã cho, ta có .
. và
và 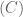 :
:
 .
.

 là điểm cố định nên
là điểm cố định nên 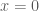 là hoành độ của
là hoành độ của  . Tức là
. Tức là  .
. lần lượt là hoành độ của
lần lượt là hoành độ của  .
. là hai nghiệm của phương trình
là hai nghiệm của phương trình 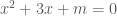
 .
.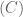 tại
tại 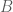 :
:
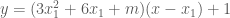
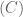 tại
tại  :
:
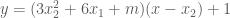
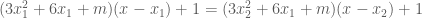
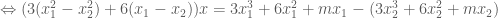
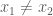 nên rút gọn thừa số
nên rút gọn thừa số  ở hai vế ta được:
ở hai vế ta được:
![[3(x_1+x_2)+6]x=3(x_1^2+x_2^2-x_1 x_2)+6(x_1 + x_2)+m](https://s0.wp.com/latex.php?latex=%5B3%28x_1%2Bx_2%29%2B6%5Dx%3D3%28x_1%5E2%2Bx_2%5E2-x_1+x_2%29%2B6%28x_1+%2B+x_2%29%2Bm&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![\Leftrightarrow [3(x_1+x_2)+6]x=3[(x_1+x_2)^2-3x_1 x_2]+6(x_1 + x_2)+m](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%5B3%28x_1%2Bx_2%29%2B6%5Dx%3D3%5B%28x_1%2Bx_2%29%5E2-3x_1+x_2%5D%2B6%28x_1+%2B+x_2%29%2Bm&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![\Leftrightarrow [3(-3)+6]x=3[(-3)^2-3m]+6(-3)+m](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+%5B3%28-3%29%2B6%5Dx%3D3%5B%28-3%29%5E2-3m%5D%2B6%28-3%29%2Bm&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
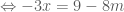
 .
.

![\Leftrightarrow 2y=\left(3[(x_1+x_2)^2-2x_1x_2)]+6(x_1+x_2)+2m \right)x-[3(x_1+x_2)((x_1+x_2)^2-x_1x_2)+6[(x_1+x_2)^2-2x_1x_2]+m(x_1+x_2)]+2](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+2y%3D%5Cleft%283%5B%28x_1%2Bx_2%29%5E2-2x_1x_2%29%5D%2B6%28x_1%2Bx_2%29%2B2m+%5Cright%29x-%5B3%28x_1%2Bx_2%29%28%28x_1%2Bx_2%29%5E2-x_1x_2%29%2B6%5B%28x_1%2Bx_2%29%5E2-2x_1x_2%5D%2Bm%28x_1%2Bx_2%29%5D%2B2&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
![\Leftrightarrow 2y=\left(3[(-3)^2-2m)]+6(-3)+2m \right)x-[3(-3)((-3)^2-m)+6[(-3)^2-2m]+m(-3)]+2](https://s0.wp.com/latex.php?latex=%5CLeftrightarrow+2y%3D%5Cleft%283%5B%28-3%29%5E2-2m%29%5D%2B6%28-3%29%2B2m+%5Cright%29x-%5B3%28-3%29%28%28-3%29%5E2-m%29%2B6%5B%28-3%29%5E2-2m%5D%2Bm%28-3%29%5D%2B2&bg=ffffff&fg=4e4e4e&s=0&c=20201002)
 chính là tung độ của
chính là tung độ của 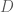

 là khoảng cách từ
là khoảng cách từ 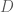 đến đường thẳng
đến đường thẳng  . Ta tính được
. Ta tính được  chính bằng chiều cao tam giác
chính bằng chiều cao tam giác  hạ từ đỉnh
hạ từ đỉnh 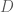 .
. theo
theo  .
. theo
theo .
. . cần tìm.
. cần tìm.
Phương trình hoành độ giao điểm của
Vì
Gọi
Ta có
và
Phương trình tiếp tuyến với
Phương trình tiếp tuyến với
HOành độ giao điểm của hai tiếp tuyến trên là nghiệm của phương trình:
Vì
Cộng hai phương trình tiếp tuyến trên cho nhau theo vế, ta có:
Ta tính được
Suy ra tọa độ của
Gọi
Tiếp theo tính đọ dài cạnh
Rồi suy ra diện tích tam giác
Cuối cùng là tìm giá trị lớn nhất của diện tích đó và suy ra
==================
Em tự làm đoạn sau nhé !
Nếu có tính toán hay rút gọn nhầm em hãy kiểm tra và sửa lại giúp thầy.
Thầy nêu hướng giải vậy thôi nhé !
ThíchThích
em cam on thay !
ThíchThích
thầy ơi thầy có phần hướng dẫn giải đề số 4 sô 415 (THTT) ko ạ . Nếu có thầy có thể cho em link để tham khảo đc ko ạ
ThíchThích
Thời gian đến, rãnh thầy sẽ giải và đăng lên để các em tham khảo.
ThíchThích
thay oi giai giup em bai nay dc k thay
trong mat phang oxy cho tam giac ABC co A(1;1) phuong trinh 2 duong cao BH va CK la x-y+1=0 va 2x+y-1=0 duong tron (C1) tiep xuc voi AB tai B va duong tron (c2) tiep xuc voi AC tai C cung cat canh BC tai M .tim toa do diem M de do dai doan noi tam 2 duong tron (c1) va (c2)
ThíchThích
em xin loi em viet thieu de a. tim M de cho do dai noi 2 tam duong tron (c1) va (c2) nho nhat thay a
ThíchThích